|
Graph
Bonjour ! Si tu es ici c’est pour commencer à apprendre à te servir de l’une des applications les plus importantes qui composent ta machine : Graph !
Sommaire :
 I – Présentation de Graph I – Présentation de Graph
 II – Fonctionnalités de base II – Fonctionnalités de base
1°.Saisir une fonction
2°.Tracer une courbe
 III – Le solveur de fonctions et sa suite d’outils III – Le solveur de fonctions et sa suite d’outils
1°.Root
2°.Maximums et minimums d’une fonction
3°.Intersections
4°.Images et antécédents
 IV – Zooms et réglages de l’écran IV – Zooms et réglages de l’écran
1°.Zooms
2°.Réglages de l’écran ou l’art du View-Window.
 V – Options et fonctionnalité secondaires V – Options et fonctionnalité secondaires
1°.Les options
2°.Les fonctionnalités secondaires
I – Présentation de Graph
L’application « Graph » permet plusieurs choses et est de ce fait un incontournable de la calculatrice Casio. En premier lieu cette application permet de tracer des courbes de fonctions, mais elle sert également à étudier les fonctions grâce à un panel d’outils performants. Elle interagit également avec d’autres applications de votre machine comme « Table » qui fera l’objet d’un tutoriel à part.
Lorsque vous êtes dans le menu principal descendez jusqu’au menu « Graph » et appuyez sur [EXE] si vous êtes fainéant ou pressé, appuyez sur la touche [5] du pavé numérique. Casio a sorti plusieurs de Graph 35 et cette touche peut varier, [3] pour les modèles les plus anciens ou [4] pour ceux un peu plus récents. Dans tous les cas vous vous retrouvez sur une interface qui ressemble à ça :
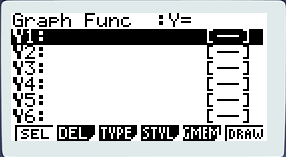
Les fonctions sont listées sur la gauche de l’écran : Y1: jusqu’à Y20: Cela signifie que vous pouvez entrer des fonctions où f(x) est l’ordonnée et x l’abscisse, nous reviendrons là-dessus plus tard. Vous pouvez également changer tout cela et nous verrons comment.
Ensuite en haut vous pouvez voir une ligne : Graph Func:… (ou Fonct Graph:… si votre machine est en français). Ce qui suit (par défaut : Y=) vous indique quel type de fonction vous allez tracer. Votre machine connait plusieurs types de fonctions différente que l’on peut exprimer sous différentes formes. Pour ce tutoriel, je vous conseille de mettre le Fonct graph en Y= par cette séquence de touches : [F3] (type) [F1] (Y=).
Pour bien comprendre comment tout cela marche, revenons un peu sur les bases des fonctions : une fonction est un objet mathématique qui associe à x, une unique image selon une formule. On note f(x) = <formule>. Sur un graphique, la courbe de la fonction est une suite de points d’abscisse x et d’ordonnée f(x). L’ordonnée peut également se noter y. Dans le cas d’une fonction affine (représentant une droite), on note f(x) = ax + b, mais l’on peut donc écrire y = ax + b. C’est pour cette raison que les fonctions de la calculatrice sont notées « Y= »…
Pour aller plus loin D’autres fonctions Ce qu’indique en fait la ligne Fonct graph c’est à quoi est égal f(x). De base Fonct graph indique Y= donc nous savons que, pour toutes les fonctions que nous allons tracer à partir de maintenant, f(x) correspond à l’ordonnée de notre repère et x à l’abscisse. Je continue encore un peu sur Fonct graph avant de passer à la suite… Si Fonct graph avait indiqué X= nous aurions ainsi sût que f(x) aurait correspondu à l’abscisse de notre repère. Nous aurions pu alors tracer des fonctions comme x = ay + b
Suffit les maths, revenons à notre Casio d’ailleurs j’ai presque terminé la présentation ! En bas vous avez les touches fonctions qui correspondent à autant de fonctionnalités que nous verrons toutes. Je passe au dernier élément de cet écran : la droite. Vous avez sans doute remarqué qu’en face de chaque Y…: il y a une sorte de trait entre crochets. Lorsque vous entrez une fonction quelconque et que vous la tracez elle s’affiche avec un trait continue d’un pixel de large dans l’écran graphique. Ce trait peut changer d’apparence et c’est à ça que sert ce petit cadre entre crochets : à vous indiquer dans quel style va être dessinée la fonction. Pour changer le style de trait, sélectionnez la fonction de votre choix et pressez [F4] (styl) puis sélectionnez un style de votre choix avec les touches [F1] à [F4]. Si vous ne voulez pas changer de style pressez [EXIT]. Changer le style peut être agréable lorsque vous avez plusieurs fonctions à l’écran comme, par exemple, une courbe et sa tangente ou plus généralement pour mieux distinguer plusieurs courbes.
Et voila, j’en ai fini pour la présentation de cette puissante application, maintenant passons aux choses sérieuses et à la pratique…
II – Fonctionnalités de base
Tout au long de ce tutoriel, nous suivrons les manipulations autour d’une fonction. Ceux qui n’ont pas le niveau risquent donc d’être un peu perdus par certains termes employés. J’essaierais donc de ne pas vous enquiquiner avec le contenu un peu technique et d’expliquer les détails mathématiques qui se cachent derrière les manipulations. Mais en général je reste sur un niveau de fin de première S. Voici la fonction sur laquelle nous allons travailler : 2x²+3x-2
1°.Saisir une fonction
Commençons par la base : comment entrer une fonction ? Il existe en fait plusieurs méthodes aussi bien par ce menu que par d’autres. De manière à ne pas tout mélanger et à ne pas vous embrouiller, je ne vous montrerais que les méthodes de saisies depuis cette application. Je vous dis ça pour que vous ne soyez pas surpris·e si vous voyez un jour que l’on peut saisir une fonction depuis un programme ou d’autres menus… Pour entrer une fonction, le plus simple reste de sélectionner la fonction désirée avec les flèches [↑] et [↓]. Puis commencez à taper votre fonction : l’écriture est automatiquement détectée. Vous pouvez aussi sélectionner la fonction puis presser la touche [→]. Un curseur clignotant apparait alors : la calculatrice est prête à recevoir la fonction.
Vous pouvez ensuite saisir votre fonction, la touche [X,θ,T] sert à entrer l’inconnue. La lettre change en fonction de votre type de fonction, ici nous avons une fonction Y= donc elle sera exprimée en fonction de x. Pour saisir les puissances vous avez une touche [x²] pour le carré et une autre à la droite de la première : [^] pour les puissances en général. Pour terminer la saisie il y a deux méthodes : soit vous voulez sauvegarder votre saisie : pressez [EXE] ; soit vous ne voulez pas sauvegarder : pressez [EXIT].
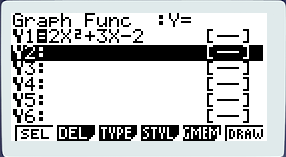
Pour ré-éditer votre fonction, il faut utiliser impérativement la seconde méthode de saisie, la première écrase la fonction déjà écrite. Pour supprimer une formule, sélectionnez-la puis pressez [F3] (del) un pop-up de confirmation va apparaître, confirmez-le. Je vous laisse saisir la fonction dont je vous ai parlé plus haut avant de passer à la partie suivante…
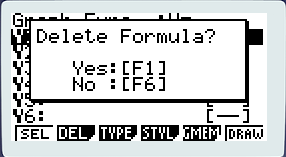
2°.Tracer une courbe
Une fois votre fonction saisie pressez [F6] (draw), votre fonction apparait à l’écran. Revenez sur l’écran de saisie via [EXIT] : maintenant, on va tracer une seconde courbe. Saisissez une fonction devant Y2: un truc bête, comme 2x par exemple. Tracez les courbes comme tout à l’heure via [F6]. Notez que presser [EXE] donne exactement le même résultat. Vos deux fonctions apparaissent à l’écran.
Mais on voit mal la droite, vous ne trouvez pas ? Pressez [F6] ou [EXIT] pour revenir à l’écran d’accueil. Là vous pouvez changer le style et revenir aux courbes. Si vous voulez avoir un résultat encore plus net, vous pouvez demander à ce que la fonction ne soit pas tracée. Revenez dans l’écran principal, sélectionnez la fonction Y2 et pressez [F1] (sel). Maintenant, le signe = n’est plus en surbrillance, donc cette fonction ne sera plus dessinée à l’écran, pour la remettre re-sélectionnez-là via [F1] (qui agit comme un interrupteur en fait).
Bon suffit les bêtises, supprimez la fonction Y2 et tracez la fonction Y1, les choses sérieuses vont commencer… Si vous ne voyez pas la courbe suivez ces instructions : dans l’écran d’accueil, pressez [SHIFT] puis [F3] (v-win) et enfin [F1] (init) avant de presser [EXE] pour valider. Nous reviendrons là-dessus plus tard. Vous pouvez faire bouger la courbe à l’écran avec les flèches.
III – Le solveur de fonctions et sa suite d’outils
1°.Root
Vous contemplez une fonction polynôme de degré deux. Ooohhhhhhh… Je vous épargne les détails mathématiques, mais en résumé. La fonction polynôme de degré deux est une fonction qui a la forme : y = ax²+bx+c. De cette fonction on peut extraire un discriminant noté Δ (delta). Ici Δ = 25. Selon des règles que vous avez vu (ou pas encore) si le Δ est strictement positif, la fonction polynôme de degré deux a deux racines c’est-à-dire qu’il existe deux points d’intersection entre l’axe des abscisses et la courbe de la fonction. Ici c’est le cas puisque la courbe passe très clairement en dessous des abscisses avant de remonter après. Dans certains exercices on demande de déterminer les coordonnées de ces deux points. Exercice simple qu’on ne vérifie pas mais avec deux calculs légèrement différents, l’erreur guette le lycéen non-averti. Pour vérifier ça c’est très simple : pressez [SHIFT] puis [F5] (g-solv). Notez que presser directement [F5] donne le même résultat. Une fois dans ce menu dont tous les détails vous seront expliqués, pressez [F1] (root). 'Root' qui signifie 'racine' en français. Cette fonctionnalité va donc vous donner gratuitement, sur un plateau les coordonnées de vos deux points et cela en un temps record ! Néanmoins, votre machine vous donne des valeurs approchées, donc apprenez le calcul !
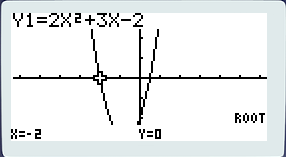
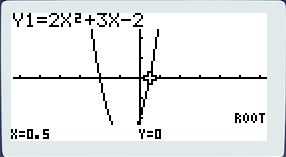
Les coordonnées de la première racine s’affichent en bas : x = -2 y = 0. Pour passer à la seconde racine pressez la flèche [→], pour revenir à la première racine, pressez la flèche [←].
2°.Maxima et minima d’une fonction
De ce même menu, la touche [F2] (max) et [F3] (min) ont des fonctions évidentes : trouver le point le plus bas (ou haut) d’une fonction. Certaines fonctions ont des extrema locaux, ces deux touches les prennent en comptes. Petit point sur les maths pour ceux que j’ai largués… Les fonctions peuvent admettre des minima ou des maxima. Sur notre fonction dessinée, vous avez une sorte de cuvette avec un point tout en bas qui correspond au point le plus bas de la fonction, on appelle ce point le minimum de la fonction. Logique !
De même si la fonction avait une bosse au lieu d’un creux, nous aurions eu un maximum, comme cette fonction : f(x) = -2x²+3x+2. Vous voila familiarisé avec le concept de maxima et minima.
En mathématiques le terme « extremum » signifie « maximum » et « minimum ». Ainsi « Trouvez les extrema de la fonction f(x) » signifie : « Trouvez tous les maxima et tous les minima de la fonction f(x) ». Le mot extremum permet donc de dire plus de choses en moins de place ! Bon maintenant les extrema locaux sont des minima ou des maxima qui existent sur un intervalle donné. Le plus simple est d’en rester là pour le moment, j’y reviendrais par la suite. Souvenez-vous juste que lorsque votre fonction admet plusieurs extremums, vous pouvez switcher de l’un à l’autre via [→] et [←].
3°.Intersections
Passons maintenant aux deux prochaines instructions soit Y-ICPT et ISCPT. Pour cette partie revenez dans l’écran d’accueil et saisissez notre fonction polynôme : 2x(^2)+3x-2 ainsi que la fonction affine : 2x-2. Tracez les deux comme on l’a vu et pressez [F5] parce que le lycéen est un animal fainéant et pressez [F4] (y-icpt).
Cette touche ne porte pas le nom « y-icpt » par hasard, « y » signifie que l’on s’intéresse aux ordonnées et « ic » est un diminutif d’intersection (c’est le même mot en anglais) et le « pt » renvoie à « point » qui est lui aussi un mot transparent. Cette fonction va donc vous donner le point d’intersection entre la courbe de la fonction et l’axe des ordonnées, tout simplement. Le problème est que vous avez deux courbes à l’écran, l’expression de la fonction sélectionnée apparait en haut et un cadre noir clignotant d’affiche sur sa courbe. Sélectionnez la courbe de votre choix avec [↑] ou [↓] puis validez avec [EXE].
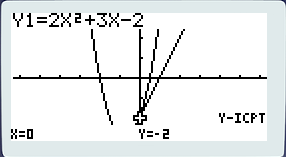
Et voila ! La fonctionnalité « iscpt » vous donne les points d’intersections entre deux courbes, ici pas de problèmes vous avez deux courbes qui se croisent deux fois, donc deux points d’intersections entre lesquels vous pouvez switcher grâces aux flèches : [←] et [→]. Dans notre cas j’ai pris soin que ces points aient des coordonnées qui tombent juste.
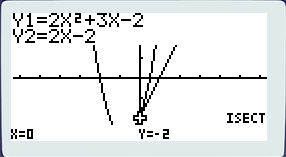
4°. Images et antécédents
Terminons avec ce menu avec les deux dernières fonctionnalités du menu « g-solv » : « y-cal » et « x-cal ». Commençons par les bases de maths… Oui encore des maths ! Oubliez pas que la calculatrice reste un outil pour les maths… Donc si je vous présente toutes les applications possibles de cet outil, il vous faut les outils mathématiques qui vont avec !
Donc une fonction associe à x une valeur. Cette valeur, notée f(x), est appelée image et x est l’antécédent de l’image. Sur un graphique cela se traduit comme cela : vous avez les images sur les ordonnées et les antécédents sur les abscisses.
La fonctionnalité « y-cal » permet de rechercher une image grâce à son antécédent. Si vous pressez [F1], la calculatrice vous demande se saisir une valeur de x, un antécédent comme on vient de le voir. La fonctionnalité « x-cal » (sur la touche [F2]) fait l’inverse : votre machine vous demande un antécédent et vous donne l’image correspondante.
IV – Zooms et réglages de l’écran
1°.Zooms
Revenons à notre fonction : 2x(^2)+3x-2 tracez-la seule et pressez [F2] pour accéder aux options du zoom. Il y en a beaucoup et nous ne verrons que les plus importantes à savoir : Box, In, Out et Orig, nous finirons par Auto.
Commençons par le début : Box ! Comme son nom l’indique (« boîte » en français) cette option permet de tracer un rectangle à l’écran grâce à deux points : le coin en haut à gauche de ce rectangle et le coin en bas à droite. La pratique ! Pressez [F1], bougez le curseur grâce aux flèches et valider le premier coin via [EXE] puis bougez le curseur à nouveau et validez le second coin via [EXE].
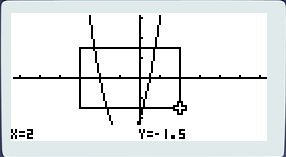
L’écran s’adapte au cadre tracé.
Pour revenir au réglage normal de l’écran, revenez dans le menu des zooms pressez [F6] (la flèche) puis [F1] (orig) cette fonction vous permet de retrouver le zoom que vous aviez au moment où vous avez tracé la courbe pour la première fois. Si vraiment vous n’arrivez pas à retrouver votre courbe, pressez [EXIT], et revenez à l’écran principal, pressez [SHIFT] puis [F3] (v-win) et enfin [F1] (init) avant de presser [EXE] pour valider. Je ne m’attarde pas plus la-dessus, j’y reviendrai très en détail dans une prochaine partie.
Maintenant revenez dans le menu des zooms et pressez [F2] (In) par défaut le curseur est situé au centre de l’écran. Vous pouvez bien entendu le bouger grâce aux flèches. Valider la position avec [EXE] ou infirmez-la par [EXIT]. Si vous validez, un zoom vers l’avant se fera dans la direction du point ciblé. Pareil avec Out qui permet de dé-zoomer.
Nous avons déjà rencontré Orig qui permet de retrouver le zoom d’origine.
Passons à Auto, disponible sur la touche [F5] dans le menu des Zooms. Cette fonction vous permet de régler automatiquement le zoom sur la courbe. Cette option est pratique si vous avez du mal à utiliser le zoom manuel. De plus votre Casio, va essayer de trouver l’endroit de la courbe le plus intéressant. Néanmoins la calculatrice est une machine (donc pas parfaite), par conséquent l’utilisation de cette fonctionnalité peut vous afficher une courbe atrocement déformée. Donc à utiliser si vraiment vous avez du mal, mais je vous recommande de maitriser les autres manières de zoomer.
2°.Réglages de l’écran ou l’art du View-Window.
Le View-Window est, par définition, la partie visible de votre écran. Pour bien comprendre, il faut savoir que votre calculatrice à un écran fini, c’est une limite physique. Au contraire, votre fonction, elle, est très grande, elle dépasse donc de votre écran. Or une calculatrice est une machine, et, comme toutes les machines, la calculatrice est bête, il faut tout lui dire sinon elle ne sait pas faire… Donc il faut lui préciser plein de choses pour qu’elle puisse bien afficher la fonction et surtout quelle partie de la fonction il faut afficher. Les paramètres par défaut sont utiles, sachez donc les remettre en place : pressez [SHIFT] [F3] (v-win) dans l’écran d’accueil ou plus simplement [F3] dans l’écran avec la courbe. Vous arrivez à ça :
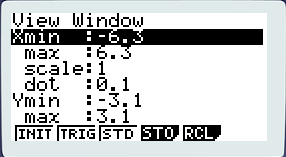
Pressez [F1] (init). Et c’est bon vous savez ré-initialiser le réglage de l’écran !
Voyons maintenant les détails…
 Xmin est la valeur minimale des abscisses Xmin est la valeur minimale des abscisses
 max est la valeur maximale des abscisses max est la valeur maximale des abscisses
 scale « échelle » en français est l’espace entre deux unités des abscisses scale « échelle » en français est l’espace entre deux unités des abscisses
La suite est la même avec Ymin, max et scale. Ignorez dot qui est un paramètre mineur que la calculatrice calcule toute seule. Les trois derniers paramètres servent aux fonctions trigonométriques que nous ne verrons pas ici.
Petite précision, scale correspond en fait à l’espace entre les graduations des axes. Donc si vous mettez scale = 1, il y aura un écart de 1 entre chaque graduation… etc
Maintenant un peu de théorie et la pratique ! Votre écran fait exactement 128 pixels de large et 64 de haut. Il est donc deux fois plus large que haut. Veillez à respecter ce rapport lors du réglage de l’écran, mais nous ferons quelques essais ensemble.
Je vous parlais plus haut des extrema et des extrema locaux. Les extrema locaux sont des maxima ou des minima qui existent sur des portions de fonctions. « Portions » n’est pas un mot mathématique, en maths, on parle plutôt d’intervalle, mais c’est la même chose : il s’agit d’un intervalle compris entre deux bornes définies.
Revenons à notre écran… Sur certains exercices on vous demande d’étudier une fonction sur un intervalle. Vous ne paniquez pas, vous savez faire, vous saisissez votre Casio et en trente secondes l’exercice est terminé. Pour cela suivez attentivement… Un intervalle (sauf avec l’infini) a deux bornes qui sont deux nombres réels. Vous avez un minimum et un maximum. Je ne les connais pas mais c’est pas grave on fera avec des chiffres après si vous voulez.
La chose à voir est la courbe, et pour bien la voir il faut connaitre son minimum et son maximum sur l’intervalle dans lequel on va étudier la courbe. Le reste est d’une simplicité… Tout est très logique, l’intervalle de l’étude va se « reporter » sur les réglages Xmin et Xmax. Le minimum de la fonction va être dans Ymin et son maximum dans Ymax. On va avoir un réglage qui va être :
Xmin : minimum de I
max : maximum de I
scale: OSEF
dot : OSEF
Ymin : minimum de f(x)
max : maximum de f(x)
scale: OSEF
dot : OSEF
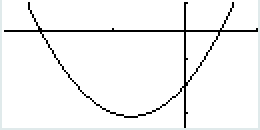
On laisse tel quel scale et dot. Dans notre cas avec notre polynôme, on veut un plan serré sur le minimum de la fonction. L’intervalle d’étude est I=[-2,5 ; 1]. Grâce à votre formidable outil, vous savez que le minimum de la fonction est à y = -3,125. On va arrondir un peu pour avoir un peu de marge à -3,5. Le maximum n’est nulle part, mais c’est pas grave, nous on veut que le bas de la courbe, en dessous des abscisses, on peut donc le mettre à 0 ou à 1 si on veut un peu de marge. Le réglage de l’écran va ressembler à ça :
Xmin : -2,5
max : 1
scale: OSEF
dot : OSEF
Ymin : -3,5
max : 1
scale: OSEF
dot : OSEF
Ça donne un truc comme ça :
Pour aller plus loin Centrer l’écran et garder les proportions de la courbe Entrez dans la fenêtre de saisie du réglage de l’écran. Saisissez le minimum de votre intervalle devant Xmin le maximum de votre intervalle devant max (dessous le Xmin) par confort réglez le scale à 1 pour un écran de taille raisonnable, si vous avez Xmin = -1000 et Xmax = 1000, il est évident que scale ne doit pas être à 1, dans ce cas 100 est plus adéquat, voire 200.
Ensuite les Y… Pour que votre écran soit équilibré il faut respecter le rapport entre la largeur et la hauteur de l’écran. Dans le cas d’une Graph 35+E (valable pour toutes les Graph 25/35/65/75/85/95 +USB/+E/SD) l’écran est deux fois plus large que haut donc Xmax-Xmin = 2*(Ymax-Ymin). Donc pour avoir un écran équilibré, vous devez tout bêtement faire le calcul suivant : (maximum-minimum)/2. Le résultat, notons-le R vous donnera la valeur à mettre dans Ymax. Pour respecter la symétrie, -R sera placé dans Ymin. Si l’on récapitule tout cela, on a un écran de View-Window qui doit ressembler à cela :
R = (maximum-minimum)/2
Xmin : minimum
max : maximum
scale: 1
dot : on s’en fout
Ymin : -R
max : R
scale: 1
dot : on s’en fout
//… Et on ne s’occupe pas la suite
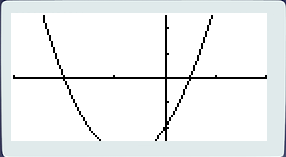
Bon suffit la théorie barbante ! Place à la pratique ! Vous avez toujours votre fonction 2x²+3x-2 à l’écran ? Non ? Alors tracez-la et pressez [F3]! Je veux étudier la fonction sur l’intervalle I=[-3 ; 2].
R = (2-(-3))/2
R = (2+3)/2
R = 5/2
R = 2,5
Donc !
Xmin : -3
max : 2
scale: 1
dot : on s’en fout
Ymin : -2,5
max : 2,5
scale: 1
dot : on s’en fout
Pour saisir les paramètres : les flèches [↑] et [↓] pour placer en surbrillance le paramètre à modifier et [→] pour commencer à saisir. Notez que presser directement une touche du pavé numérique écrase l’ancienne valeur au profit de celle saisie. Pour quitter la saisie : [EXE] pour sauvegarder, [EXIT] pour sortir sans sauvegarder. Et même méthode pour quitter le réglage de l’écran. Si vous avez bien tout suivi, vous devriez avoir un zoom propre sur les deux racines de votre polynôme !
V – Options et fonctionnalités secondaires
1°.Les options
Commençons par les options ! Que vous soyez dans l’écran d’accueil ou en train d’observer une courbe ne change rien : pressez [SHIFT] puis [MENU] (Set Up). Pour quitter ce menu, pressez [EXIT] ou [EXE]. Si vous n’avez rien modifié, [EXIT] vous renverra sur l’écran dont vous êtes venu, sinon vous serez renvoyé à l’écran d’accueil.
Les premières options sont des options de présentations. Je vous déconseille fortement d’y toucher sauf si votre professeur vous explique en détail comment tout cela marche. En général, les professeurs ne vous expliquent pas tout et c’est pour ça que vous êtes en train de lire ce tuto. En bref, Input/Output est le mode d’entrée du clavier, la notation normale est Math (ce mode permet, entre autres d’avoir des fractions bien présentées et des jolies puissances) si la ligne affiche Linear soulagez vos neurones et pressez [F1] pour avoir un texte propre.
La ligne suivante Draw type vous permet de sélectionner le type de tracé : des points seuls ou des points reliés, pour bien voir votre fonction, je vous conseille de mettre Connect via [F1] qui produit une courbe plus visible.
Ineq type permet de régler le type des inéquations : And ou Or par défaut c’est réglé sur And laissez-le comme ça sauf indication contraire de votre professeur.
Laissez Graph Func sur On.
Nous reviendrons en détail sur Dual Sreen qui est une option très puissante.
Simul Graph pour « Graphes simultanés » est une option qui ne sert à… rien ! Enfin, si elle sert à choisir si vous voulez afficher toutes les fonctions sélectionnées en même temps. Je vous déconseille de l’activer pour plusieurs raisons : tout d’abord, cette fonction trace toutes les fonctions sélectionnées en même temps, donc vous ne savez plus à quelle équation correspond quelle courbe. Lorsque vous tracez les fonctions une par une, la calculatrice affiche en haut de l’écran la fonction en cours de dessin ça peut être un avantage. La deuxième raison est que le gain de temps est en fait limité : la calculatrice doit tracer les deux courbes en même temps et cela lui demande plus de ressources. Donc en conclusion, autant laisser ça sur Off via [F2].
« Derivative » affiche la dérivée d’un point de la courbe. Vous pouvez en faire ce que vous voulez, cette option occupe un peu de place en bas à droite de l’écran, au-dessus de l’ordonnée du point sélectionné.
Laissez Background réglé sur None.
Les options suivantes sont évidentes et ne concernent presque que l’aspect de votre écran, je vous laisserai le soin de les modifier comme vous le souhaitez. Angle modifie l’unité d’angle. Complex Mode permet de switcher entre les différents type de nombres complexes, mais vos professeurs de Terminale vous expliquent ça.
Coord permet d’afficher les coordonnées du point sélectionné en bas de l’écran. Sur les courbes tracées vous pouvez la suivre point par point via [F1] (trace).
Grid permet d’afficher des points atrocement moches qui symbolisent la grille de l’écran, je déconseille fortement cette option qui rend l’écran illisible !
Axes permet d’afficher (ou pas) les axes du repère, cela vous permet d’avoir un repère sur la taille de la courbe.
Label affiche x et y a côté des axes correspondants ça ne sert à… rien donc je vous conseille de laisser cette option désactivée pour bénéficier du maximum de place sur votre petit écran.
Laissez Display sur Norm1. Cette option correspond à la méthode d’affichage des nombres : scientifiques pour les puissances de 10 et notation ingénieur pour avoir les lettres : 10 K par exemple.
Bon, on a tout vu ! Reste cette fameuse option : Dual Screen… elle sert à scinder votre écran en deux. Vous pouvez, au choix, choisir d’avoir deux courbes différentes (via [F1]) ou une courbe et un tableau de valeur (via [F2]) ou alors un seul écran via [F3]. Commençons avec les deux courbes… Pressez [F1] puis quittez le menu des réglages et tracez la courbe de référence qui ne nous a pas quitté du tuto. Notre courbe s’affiche à gauche et l’écran de droite reste vide. Vous pouvez vous déplacer et zoomer comme vous le voulez, mais que sur l’écran de gauche. Celui de droite reste vierge et immobile. La technique consiste à utiliser deux nouveaux outils en votre possession : pressez [OPTN] et [F2] (swap). Cette commande vous permet de switcher les deux écrans : celui de gauche va à droite et vice-versa. Et [OPTN] puis [F1] (copy) permet de copier l’écran de gauche dans celui de droite. Cela écrase le contenu de l’écran de droite. Cependant cette fonction ne fait rien si l’écran de gauche est vide. Maintenant, passons à la pratique : mettez la courbe à gauche et effectuez un zoom sur un point précis via l’outil Box le résultat du zoom apparait à droite !
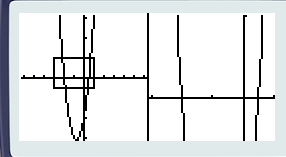
Ensuite grâce à swap vous pouvez naviguer dans le zoom tout en gardant une vue d’ensemble de la fonction à droite.
Le deuxième dual screen avec graphe et tableau est expliqué dans la partie suivante.
2°.Les fonctionnalités secondaires
Il y a plusieurs fonctionnalités secondaires. Comme je l’évoquais dans la partie précédente l’option dual screen fonctionne avec la fonctionnalité Trace qui permet de suivre la courbe avec un curseur dont les coordonnées sont affichées en bas de l’écran. Réglez le Dual Screen sur G to T (Graph to Table) tracez la courbe pressez [SHIFT] puis [F1] ([F1] direct marche aussi). Une croix apparait à l’écran. Vous pouvez la faire suivre la courbe avec les flèches [←] et [→]. Pressez [EXE] pour enregistrer les coordonnées actuelles et les stocker dans le tableau. Par exemple, vous pouvez vous rendre sur les racines du polynôme et les enregistrer dans le tableau.
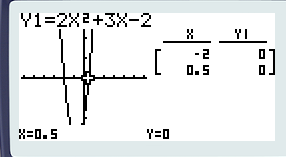
Ensuite pressez [OPTN] et avec [F1] (chng), vous pouvez switcher entre la courbe et le tableau. Une fois dans le tableau vous pouvez tout supprimer via [F2] ou supprimer juste une ligne avec [F1]. Pressez à nouveau [OPTN]. On retrouve le [F1] (chng) pour re-basculer sur la courbe. Mais aussi d'autres fonctionnalités comme [F2] (lmem) qui permet de stocker la colonne dans laquelle est la case en surbrillance dans une liste.
Passons aux fonctions de dessins, ces fonctions permettent de dessiner sur la courbe à l’écran. Pressez [F4], toutes les fonctions sont intuitives, je ne vous en présenterai qu’une : Tang qui sert à tracer des tangentes… pressez [F2] (tang). Naviguez sur la courbe comme avec Trace et validez avec [EXE] pour tracer la tangente. C’est là qu’intervient l’option que nous avons croisée : Sketch Line. En effet, le menu de la touche [F4] s’appelle… « Sketch » cette option permet donc de modifier le style de trait des fonctions de dessins. Dans ces foncitons [F1] (Cls) permet d’effacer l’écran de tous les dessins, mais laisse la courbe (Cls signifiant : Clear Screen).
Je vous présente rapidement ce menu quand même mais c’est rapide : passez avec [F6] à la page suivante. Line permet de tracer des lignes entre deux points spécifiés, utilisez F-Line plus simple et rapide). Crcl permet de tracer des cercles, vous devez sélectionner un premier point (le centre) et un second (le rayon). Vert sert à tracer une droite verticale. Il en va de même avec Hztl (horiontal). PEN est l’outil de crayon baissez et relevez le stylo avec [EXE]. Text vous permet d’afficher du texte aux coordonnées du curseur. Il vous suffit de taper le texte (les lettres minuscules et majuscules sont gérées.
Il me reste une toute petite astuce ! Lorsque vous voulez tracer une tangente à un point d’abscisse connue Tracez la courbe et pressez une touche du pavé numérique. Une fenêtre pop-up vous saute à la figure en vous demandant une valeur de x validez avec [EXE] ou infirmez avec [EXIT]. Si vous validez le curseur se placera sur le point de la fonction d’abscisse x donnée.
Une autre application secondaire réside dans les fonctions définies sur des intervalles précis. La syntaxe est très simple :
<fonction> (<intervalle>)
Pour la fonction, vous savez comment l’entrer, pour l’intervalle, il faut spécifier les valeurs de x sur lesquelles la fonction est définie. Par exemple, si l’on entre :
x² (x<3) la calculatrice va tracer la parabole x² pour tous les x strictement inférieurs à 3. Les opérateurs permettant de déclarer l’intervalle sont cachés dans le menu programme du catalogue : pressez [SHIFT] [4] (catalog) [F6] (ctgy) pour catégories, [5] (commande prgm). Et là vous sélectionnez les opérateurs qui vous intéressent.
Et voila j’ai terminé ce tutoriel sur l’utilisation de l’application Graph !
|
|
