|
Tutoriel rédigé le : 2022-04-12 10:31 par Lephenixnoir Catégorie : Tutoriels du Mercredi Calculatrice : Toutes
Discutez de ce tutoriel sur le forum >> Voir le sujet dédié (7 commentaires)
TDM 22 : Optimisations de stratégie en Basic
Le Tutoriel du Mercredi (TDM) est une idée proposée par Ne0tux, qui recouvre tous les usages de la calculatrice - des applications de Casio à la conception de jeux en passant par la production artistique.
Aujourd'hui, on s'intéresse à des optimisations en temps et espace de programmes Basic !
Niveau ★ ★ ★ ☆ ☆
Tags : Listes, Complexes, Équations, Probabilités, Basic
Bienvenue, chers lecteurs, dans cette 22ème édition du TDM. Avec le déroulement animé de la 1kBCJ#4 et de la 1kBCJ#5, j'ai eu l'occasion de refaire un peu de Basic récemment, et je voulais profiter de l'occasion pour partager des stratégies d'optimisation. Les techniques que je présente ici ont été utilisées dans mes participations (Fiery Fighter et Prison Gelée), donc je m'en servirai d'exemples concrets pour ne pas juste parler de code.
La plupart des optimisations répandues en Basic sont locales et correctes : omission de parenthèses fermantes (gain d'espace), usage de List1...List6, ⇒ (réduction du temps de lecture du code), stockage dans les variables de valeurs redondantes (gain de temps d'évaluation)... toutes ces astuces sont locales parce qu'elles agissent à petite échelle et ne nécessitent pas de comprendre le programme entier pour fonctionner ; et elles sont correctes car elles ne changent pas le comportement du programme.
Les optimisations qui m'intéressent ici, et que j'appelle « optimisations de stratégie » (ce n'est pas un terme technique), consistent à modifier le modèle du programme et son calcul quitte à modifier son comportement en échange d'un gain d'espace ou de performances plus conséquent. 
De façon générale, je trouve que ce sont des transformations difficiles à faire sur des programmes déjà finis, car il est compliqué de changer le comportement d'un programme bien poli. À la place, je les trouve utiles durant le prototypage, à un stade où on peut encore se permettre de modifier le concept du programme en échange de meilleurs performances.
Sur ce, à l'attaque ! En plus des stratégies je rappellerai quelques mécanismes, qui sont les outils Basic performants que l'on veut utiliser et qui motivent les stratégies.
Mécanisme : calcul parallèle sur les listes
On ne présente quasiment plus le « calcul listique », une forme de calcul sur les listes que possède le Basic Casio. (Pour la petite histoire, le terme est apparu sur le forum ; « monadique » serait plus précis mais trop pédant, et à défaut d'une bonne alternative, on continue d'employer l'original.)
Calculer avec tous les éléments d'un coup. Le principe est simple : une seule opération utilise ou modifie tous les éléments d'une liste à la fois. Par exemple, l'opération « carré » (²) est étendue aux listes et peut calculer le carré de tous les éléments d'une liste à la fois.
{1,2,3,4,5→List 1
List 1²→List 1 # = {1,4,9,16,25}
Ce calcul produit le même résultat que stocker à la main le carré de chaque élément.
For 1->I To Dim List 1
List1[I]²→List 1[I]
Next
Ce qu'on peut voir aussi, et c'est un avantage qui n'est pas évident quand on pense juste aux opérations, c'est que si on ne spécifie pas de destination le résultat est stocké dans List Ans, ce qui évite d'avoir à créer une nouvelle liste si on a besoin de conserver l'originale.
# Avec le carré étendu et List Ans
List 1²
# Avec le carré étendu, sans List Ans
List 1²→List 2
# Sans le carré étendu
Dim List 1
Ans→Dim List 2
For 1→I To Ans
List 1[I]²→List 2[I]
Next
L'usage des opérations étendues sur les liste est crucial pour optimiser à la fois la vitesse du programme et sa taille. Les boucles sont naturellement les parties les plus chargées des programmes, donc les éliminer au profit de calculs sur les listes est presque toujours bénéfique. Quant à l'espace, le gain est évident. Sans compter que moins il y a de code plus ça va vite en général (Basic oblige).
Combinaisons de listes et de constantes. Le calcul sur les listes ne se limite pas qu'aux listes entre elles : on peut aussi utiliser des constantes dans les opérations.
{1,2,3,4,5→List 1
2List 1+7→List 1 # = {9,11,13,15,17}
Ça marche même avec des constantes complexes (détaillées ci-dessous), ce qui permet à une très vaste classe de tâches d'être optimisée avec du calcul parallèle sur les listes. 
Aperçu rapide des fonctions. Il faudrait rentrer dans beaucoup de détails pour donner une vue exhaustive de toutes les opérations qu'on peut faire sur les listes, mais vous pouvez avoir une intuition avec les quelques outils suivants :
- Réductions : Min(), Max(), Sum (parfois utiles : Mean(), Median(), Prod)
- Génération de listes : Seq(), Augment()
- Arithmétique : + - × ÷, Int÷, Rmdr, Abs
- Opérations logiques : comparaisons, And, Or, etc
- Essentiellement toutes les fonctions courantes sur les réels et complexes
C'est tellement puissant qu'en fait si vous pouvez représenter votre calcul comme la répétition uniforme d'un calcul unique sur plein de valeurs, alors vous pouvez presque automatiquement le paralléliser et exploser les performances ! 
Vous savez peut-être (c'est un peu le méta en Basic) que la majorité du temps passé dans l'exécution d'un programme par PRGM est dans la lecture du code (ou, si vous faites beaucoup de dessin, dans le rafraîchissement permanent de l'écran). Une des stratégies quasi-universelles est donc d'utiliser les instructions les plus puissantes possibles pour faire le maximum de travail avec le minimum de code.
Le calcul sur les listes atteint très élégamment cet objectif en exprimant avec peu de code ce qu'on veut calculer. Ainsi, au lieu de perdre du temps à lire les instructions entre le For et le Next des dizaines de fois, PRGM va utiliser une boucle for codée directement dans l'interpréteur, qui va beaucoup plus vite, surtout si les calculs à faire sont intensifs.
Stratégie : privilégier les comportements homogènes
Pour pouvoir mettre en oeuvre le calcul parallèle sur les listes, il faut éviter les exceptions : tous les éléments de la liste doivent avoir le même rôle pour qu'on puisse faire un seul calcul pour tout le monde, sinon on se retrouve à gaspiller du temps et du code précieux à gérer les cas particuliers.
Pour donner un exemple qui marche bien, dans Fiery Fighter, il y a une petite dizaine de projectiles dont la position est stockée dans deux listes, List1 pour les abscisses et List2 pour les ordonnées. Le joueur est à la position A,B. On veut calculer s'il y a une collision, à savoir un projectile à moins de 3 pixels du joueur, et le calcul parallèle sur les listes trivialise complètement la tâche :
Abs (List1-A+i(List2-B
3>Min(List Ans⇒Goto L
En plus des listes il y a un peu de complexes là-dedans (j'en reparle plus tard), mais vous pouvez voir que le calcul parallèle est utilisé 5 fois sur la première ligne :
- List1-A et List2-B calculent la position des projectiles par rapport au joueur (2 opérations) ;
- ...+i(... donne un complexe (vecteur) qui combine la position en abscisse/ordonnée (2 opérations) ;
- Abs ... calcule la distance au joueur (1 opération).
À la fin de la première ligne on obtient donc dans la List Ans la distance entre le joueur et chaque projectile, et ensuite on regarde si le plus près est à moins de 3 pixels.
Il y a un autre exemple parlant dans Prison Gelée, concernant la génération de la map. Cette fois il n'y a pas de calcul direct sur les listes, mais il y a une boucle qui est grandement simplifiée en évitant les cas particuliers. Dans ce jeu, la map est découpée en trois faces carrées de 5x5 :
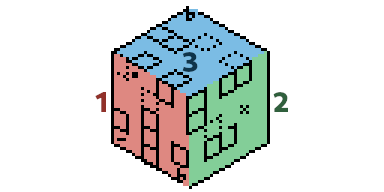
La map est stockée sous la forme suivante, avec les 3 faces côte-à-côté (sur la face 3 les lignes sont en direction de la face 2, les colonnes en direction de la face 1).
40010 10110 20000
00400 10000 00404
00100 04080 11000
10101 01100 00000
60102 00000 01010
Pour dessiner la map il faut regarder toutes les cases voisines et mettre un trait là où il y a des murs. Le problème se pose au niveau des transitions de face, particulièrement celles de la face haute (la 3). Visuellement, le bord bas de la face haute donne sur la face gauche (la 1), mais dans la matrice la face 1 est tout au début. Visuellement, le bord droit de la face haute (qui est vertical) donne sur la première ligne de la face droite (qui est horizontale). Pour accéder aux bonnes informations dans la matrice, il y a donc pas mal de petits calculs à faire pour trouver quelle case est à côté de quelle case, ce qui est à la fois fastidieux et lent.
L'alternative qui est employée dans Prison Gelée consiste à dupliquer l'information pour la mettre à la place attendue. La matrice est étendue comme ceci :
40010 10110 20000 0
00400 10000 00404 1
00100 04080 11000 1
10101 01100 00000 0
60102 00000 01010 1
..... ..... 40010
Ainsi la première ligne de la face 1 est dupliquée sous la face 3, et la première ligne de la face 2 est dupliquée et recopiée à droite de la face 3. (Les points sont des valeurs quelconques inutilisées par le programme.) Avec cette modification, le dessin devient beaucoup plus facile, parce qu'on peut trouver toutes les cases adjacentes en regardant à droite en bas dans la matrice sans se soucier des conditions de bord, ce qui est à la fois plus rapide et économe en espace.
Mécanique : Calcul vectoriel avec des complexes
Je sais qu'on en parle beaucoup, mais utiliser les complexes pour faire des coordonnées 2D est un des outils le plus pétés en Basic. C'est parce la théorie mathématique des nombres complexes est incroyablement riche, et contient énormément d'opérations utiles qui sont très utiles pour bouger des objets dans le plan. Elle a aussi des liens extrêmement forts avec la théorie des vecteurs 2D et donc on peut s'en servir pour faire plein de géométrie. 
Des paires de réels. L'intuition la plus simple c'est de voir un nombre complexe comme une paire de nombres réels. Le premier est appelé partie réelle du nombre complexe, et le second est appelé partie imaginaire. On pourrait écrire la paire (x,y), mais on préfère utiliser un nombre spécial noté i et écrire x+iy. Le nombre i n'est pas un réel donc on ne peut pas simplifier iy (un peu comme si j'écrivais « x pommes + y tomates », on ne peut pas mélanger les deux).
Bien sûr si vous avec deux nombres vous pouvez toujours les interpréter comme les coordonnées d'un point du plan, comme sur la figure de gauche ci-dessous. On appelle ça des coordonnées cartésiennes, et du coup x+iy est appelé la forme cartésienne d'un nombre complexe.
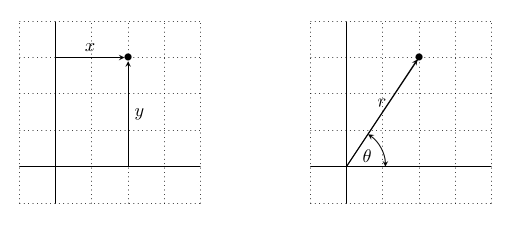
Formes cartésienne et polaire d'un nombre complexe.
Ce n'est pas tout, cependant. Un point du plan vous pouvez aussi le désigner par la distance qui le sépare de l'origine (appelée rayon et notée r), combinée avec l'angle entre la direction du point et l'axe horizontal (noté θ), comme sur la figure de droite. On appelle ça les coordonnées polaires, et il y a aussi une forme polaire des complexes, qu'on écrit r∠θ. (Pour les curieux, c'est juste une notation pour le nombre complexe r·e^(iθ). Mais là ça devient compliqué.)
Le fait que les complexes aient ces deux formes montre déjà à lui tout seul qu'on peut utiliser les complexes pour calculer des positions dans le plan (avec x et y), des mouvements (aussi avec x et y), des distances (avec r), et des angles (avec θ).
Opérations de corps. Sans rentrer trop dans les détails, vous pouvez additioner, multiplier et diviser les nombres complexes, et toutes les propriétés dont vous avez l'habitude marchent (commutatitivé, associativité, distributivité, etc).
Si vous additionez x+iy avec z+it, vous récupérez, sans trop de surprise, (x+z)+i(y+t). Ce que ça veut dire c'est qu'une seule addition de complexe peut faire deux additions de nombres réels. On peut donc, par exemple, stocker dans une variable la position d'un objet sous forme de complexe, dans une autre sa vitesse, et faire une seule addition pour calculer le déplacement.
64+32i→P # L'objet est à la position (64,32)
3+5i→V # On se déplace de 3 pixels/frame en X, 5 pixels/frame en Y
P+V→P # Pouf, déplacement fini !
Ça peut sembler anodin avec un seul point mais ça devient redoutable quand on fait des listes de complexes et qu'on remplace les additions par des opérations parallèles sur ces listes. Oui les stratégies de ce tutoriel se combinent ! 
Pour information, il y a quatre fonctions qui permettent de calculer les coordonnées (et qui marchent sur les listes) : ReP calcule x, ImP calcule y, Abs calcule r, et Arg calcule θ. Vous pouvez totalement créer un complexe dans sa forme cartésienne et ensuite récupérer r/θ (calcul de distance/angle entre deux objets), ou créer un complexe dans sa forme polaire et ensuite récupérer x/y (calcul de trigonométrie et tracé, parce que oui il y a aussi de la trigonométrie là-dedans). 
Stratégie : coordonnées dans le plan avec des complexes
Les complexes sont utiles pour calculer dans le plan y compris dans des situations inattendues. Par exemple, le bord du cube dans Prison Gelée forme un hexagone régulier. On le dessine en Super DrawStat en même temps que les murs, et donc on a besoin de calculer la position des 6 points de cet hexagone. Eh bien ça se fait avec des complexes et du calcul sur les listes !
1∠(π{1,3,5,7,9,11,1}÷6→List1
La plupart des usages utiles des complexes proviennent du fait qu'avec une seule variable, ou une seule liste, on peut stocker les positions à la fois en abscisses et en ordonnées, et donc chaque calcul fait plus de travail. Dans ce cas on utilise juste les coordonnées cartésiennes, ce qui est déjà pas mal, et donne de bons résultats. Par exemple une fois la List1 crée comme ci-dessous et étendue pour contenir les murs, on peut la dessiner en une seule ligne comme ceci.
Graph(X,Y)=(ReP List1[T],ImP List1[T
Mais pour donner un autre exemple assez fort, dans Fiery Fighter il y a régulièrement des projectiles créés qui volent dans la direction du joueur à une vitesse choisie aléatoirement.
Ici, le joueur est à la position (A,B) et le projectile apparaît à la position E (complexe). Le projectile doit avoir une vitesse de 3Ran# +1 et aller dans la direction du joueur. On calcule A+iB-E pour connaître la position relative du joueur et du projectile, ensuite on obtient l'angle avec Arg et on utilise la notation ∠ pour créer le vecteur vitesse à partir de cet angle et de la vitesse aléatoire.
(3Ran# +1)∠Arg (A+iB-E→List 7[I
On obtient un complexe dont la partie réelle (le x) est la vitesse horizontale du projectile, et la partie imaginaire (le y) est la vitesse verticale. Cette information est réutilisée à chaque tour pour calculer la nouvelle position des projectiles par une simple addition.
ReP List 7+List1→List1 # Abscisses
ImP List 7+List2→List2 # Ordonnées
Et ainsi, on passe des coordonnées cartésiennes (A,B et E) aux polaires (vitesse/angle) aux cartésiennes (position/vitesse), ce qui permet de programmer sans effort une mécanique de jeu pas tout à fait évidente. 
Projections, déformations, perspectives. J'ai mentionné que la théorie des nombres complexes se rapprochait beaucoup de celle des vecteurs 2D. Ce n'est pas un hasard, et on pourrait passer des heures à détailler toutes les raisons mathématiques qui provoquent ce lien. Mais pour l'instant j'ai surtout parlé des complexes et pas beaucoup des opérations vectorielles.
Parmi les choses utiles que la théorie des vecteurs (ou algèbre linéaire pour les intimes) apporte, il y a de quoi faire des rotations et déformations du plan. Pour reprendre l'exemple du cube de toute à l'heure, il y a 3 faces planes avec 3 « projections » différentes. Dans le code le dessin est fait en 2D normalement et ensuite une transformation est appliquée pour déformer le résultat pour donner l'effet 3D. Ça prend quelques multiplications, le plus long c'est d'indiquer pour chaque face la position du coin haut droite et les directions horizontale et verticale.
Bien comprendre les complexes (... et l'algèbre linéaire) est assez difficile mathématiquement parlant, mais il y a pas mal de choses utiles qu'on peut apprendre à faire avec un peu de pratique, et ça devient vite un outil incontournable. 
Stratégie : simplifier les boucles critiques
J'ai mentionné plus haut qu'optimiser en espace aide à optimiser en temps. C'est parce que le code n'est pas compilé ; PRGM passe son temps à lire les instructions, chercher les retours à la ligne, et chercher les fins de blocs. Par exemple, si vous avez une condition qui est fausse dans un If, PRGM va quand même devoir lire tout le code du If pour déterminer s'il y a un Else et trouver le IfEnd.
Ça veut dire qu'on ne peut pas se contenter de regarder le code exécuté pour optimiser la vitesse d'un programme, il faut aussi regarder le code non exécuté. Et sur ce point, les structures de contrôle habituelles (If, For, While, etc) ne sont pas bonnes parce que tout le code est à l'intérieur du bloc.
Pour qu'une boucle critique tourne rapidement il faut descendre le plus vite possible du haut vers le bas et maximiser le temps passé à faire des choses utiles. Lire du code qui n'est pas exécuté n'est pas utile, donc le code qui n'est pas exécuté souvent ne doit pas être dans la boucle critique.
Dans Fiery Fighter, la boucle critique déplace le joueur, les missiles, et calcule les collisions entre le joueur, la map, et les missiles. Le joueur n'attaque pas souvent, donc le code n'a pas besoin d'être dans la boucle. Les missiles n'apparaissent pas souvent, donc le code n'a pas besoin d'être dans la boucle. Et le joueur ne peut mourir qu'une fois donc évidemment ce code-là n'est pas dans la boucle non plus.
À la place, les conditions sont calculées et le code détaillé est lié via un label.
While 1
...
Collision⇒Goto C
Lbl D
...
WhileEnd
Lbl C
...
Goto D
De cette façon, lorsque la condition n'est pas remplie (ie. quasiment tout le temps), la boucle critique peut continuer immédiatement sans avoir à lire tout le code du Lbl C, ce qui prend du temps même s'il n'est pas exécuté. 
Cette technique est la plus notable que j'ai à mentionner en rapport avec les boucles critiques spécifiquement, mais bien sûr réduire la taille du code exécuté avec n'importe laquelle des techniques précédentes est tout aussi important.
Stratégie : utiliser des objets définis par des équations
Le Basic est très orienté maths, et il est assez facile de faire des calculs compliqués avec peu de code tant qu'ils rentrent dans un cadre mathématique. Par exemple, la map de Fiery Fighter a 5 côtés qu'on peut représenter par des droites :
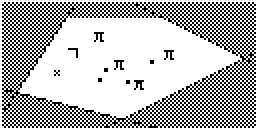
- y ≤ 1.5x + 6
- y ≤ 56
- y ≤ -0.5x + 96
- y ≥ -0.25x + 20
- y ≥ 0.5x - 26
Pour chaque droite, j'ai noté si c'est les valeurs de y au-dessous (≤) ou au-dessus (≥) de la droite qui sont dans la map. On peut représenter toutes les droites avec 3 listes : une pour le coefficient de x, une pour le coefficient constant, et une pour la direction.
{1.5,0,-.5,-.25,.5→List4
{6,56,96,20,-26→List5
{1,1,1,0,0→List6
Comme on peut utiliser des comparaisons dans le calcul parallèle sur les listes, on peut déterminer assez facilement si une position (A,B) est du bon côté de chaque droite :
AList4+List5≥B≠List6
Ce calcul donne une liste où chaque valeur vaut 0 si le point (A,B) est du bon côté de la droite et 1 sinon. Pour savoir si le point (A,B) est dans la map il faut tester s'il y a un 1 dans la liste. Il y a plusieurs moyens de faire ça, par exemple en ajoutant toutes les valeurs :
0=Sum(AList4+List5≥B≠List6 # = 1 si (A,B) est dans la map, 0 si collision
Le résultat de ce calcul est utilisé pour gérer les collisions joueur/map. Dans le jeu, on est en (A,B) et on veut savoir si on peut aller en (A+2C,B+2D), donc le test se fait à cet endroit-là. Si le test renvoie 1, on met à jour la position.
0=Sum ((A+2C)List4+List5≥B+2D≠List6
A+2CAns→A
B+2DAns→B
Voyez le peu de code nécessaire pour le système complet de déplacement/collisions du joueur ! 
Stratégie : actions probabilistes
L'aléatoire est un outil très polyvalent. On s'en sert le plus souvent dans les jeux, pour donner de la variété, mais on peut aussi s'en servir pour optimiser en réduisant la quantité de travail à faire.
Dans Fiery Fighter, la liste des projectiles a une taille fixe, et les projectiles sont « recyclés » quand ils sortent de la map pour pouvoir être re-tirés plus tard. Il faut donc collecter les projectiles quand ils sortent de la map, ce qui se fait par un calcul de collision.
Le calcul de collision utilise des listes pour tester tous les bords de la map en même temps (voir la partie précédente), donc on ne peut pas en plus tester tous les projectiles en même temps. Mais tester les 8 projectiles individuellement à chaque frame (0.5s environ) est beaucoup trop long, surtout qu'ils ne sortent pas souvent de la map.
Chacun son tour, au hasard. Une solution à ce problème est de tester aléatoirement un projectile à chaque frame. Comme ça on réduit drastiquement le temps de calcul, et comme le générateur aléatoire est « équilibré » tous les projectiles sont testés régulièrement. Du coup les projectiles peuvent rester quelques temps hors de la map avant d'être testés et recyclés, mais ce n'est pas grave. Le temps de calcul économisé permet d'ailleurs d'en rajouter !
Bien sûr, ce n'est possible que pour les actions qui sont assez rares et assez peu importes. Hors de question de faire ça pour tester les collisions avec le joueur par exemple, parce que tous les projectiles qu'on ne regarde pas seraient libres de passer à travers le joueur ! 
Conclusion
Voilà qui conclut ce tour d'horizon de quelques « optimisations de stratégie » en Basic. Même si la plupart d'entre elles ne nécessitent pas de modifier le comportement du programme, j'ai trouvé que c'est bien plus facile de les mettre en oeuvre si le programme est conçu et ajusté pour bien les utiliser. J'espère que ça servira pour les prochaines 1kBCJ ! 
À bientôt sur Planète Casio ! 
Discutez de ce tutoriel sur le forum >> Voir le sujet dédié (7 commentaires)
|
|
