|
Tutoriel rédigé le : 2006-11-19 11:30 par Neuronix Catégorie : Basic Casio Calculatrice : Graph 35 à 100
Discutez de ce tutoriel sur le forum >> Voir le sujet dédié (121 commentaires)
Créer un programme 3D
Tout programmeur en basic se pose la question de la "3D" ...qui sonne si mystérieusement et délicieusement à l'oreille de tout accro du monde virtuel.
Je propose ici une approche d'une methode de rendu d'objets en 3D. Si vous etes un programmeur courageux et ambitieux passez votre chemin, regardez mes progs Util 3D et graph 3D sans regarder le code et cherchez vous meme 
Je vais enployer la méthode du drawstat, pensez à regarder le tutorial dédié à cette technique si vous n'etes pas au point :).
On va travailler sur un objet simple : un cube de 2 unités de coté centré sur l'origine.
Entrons ses coordonnées :
{1,1,-1,-1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,1}->List 1
{-1,1,1,-1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1}->List 2
{-1,-1,-1,-1,-1,1,1,-1,1,1,-1,1,1,-1,1,1}->List 3
Notez que pour avoir un beau cube avec tous ses aretes en drawstat il faut repasser par certains pouints d'ou le nombre de points.
Ici List 1 = X List 2 = Y et List 3 = Z
Nous allons partir du principe que pour afficher le cube en 3D il suffit de retenir ses coordonnées en X et Y. Donc essayons d'afficher notre cube :
//paramétrez le s-graph 1 pour le drawstat en xyLine et Dot
S-WindMan // pour que nous puissions imposer la fenetre
View-Window -4,4,0,-2,2,0 // on peux prendre cette fenetre pour l'exemple car avec le coté du cube est de longueur 2
Drawstat
Et là on obtient :
On dirait un carré et pas un cube car on n'a pas ajouté d'effet de fuite. On fera ça plus tard, pour le moment on va faire tourner le cube sur lui meme 
On a les coordonnées cartésiennes des points du cube mais on va utiliser les coordonnées polaires pour la démonstration de la formule que j'ai utilisé qui est sans doute la plus rapide et la plus simple.
On va faire tourner le cube selon le plan x-y puis y-z puis x-z donc en fait à chaque fois on est ramené à une rotation simple dans un plan tel que vous en connaissez depuis la seconde (au moins).
Regardez l'image suivante pour mieux comprendre ce qui suit :
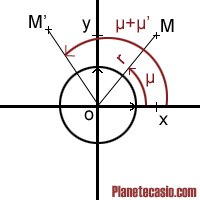
Le point initial M fait un angle µ avec l'axe des abscisses et est à une distance r de O.
M' le point image apres la rotation est également à une distance r mais fait un angle µ+µ' avec l'axe des abscisses où µ' est l'angle de rotation.
On donc en coordonnées polaires : M(r;µ) M'(r,µ+µ') et en coordonnées cartésiennes M(x,y) et M'(x',y')
On a :
x = r*cos µ x' = r*cos (µ+µ')
y = r*sin µ y' = r*sin (µ+µ')
J'imagine que vous connaissez tous tres bien vos formules de trigo donc je ne vous rappelle pas que
cos (a+b) = cos a*cos b - sin a*sin b
sin (a+b) = sin a*cos b + sin b*cos a
D'où
x' = r*cos µ*cos µ' - r*sin µ*sin µ'
= x*cos µ' - y*sin µ'
y' = r*sin µ*cos µ' + r*sin µ' *cos µ
= y*cos µ' + x*sin µ'
Et voila ! on a une magnifique formule en fonction de x, y et µ' l'angle de rotation!!!!
Simple et extremement rapide! car il suffit de 2 calculs par rotation!
J'ai mis beaucoup beaucoup de temps pour trouver ceci meme si la formule parait simple une fois ecrite il faut y penser...
Voila, je ne vous fais pas le code, je vous laisse gratter un peu quand meme et au passage vous venez de lire en 2 min ce que j'ai cherché pendant des mois...1 an je pense :(.... (car MOI je voulais faire tout seul )
Code d'exemple :
ClrGraph
{1,1,-1,-1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,1}->List 1
{-1,1,1,-1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1}->List 2
{-1,-1,-1,-1,-1,1,1,-1,1,1,-1,1,1,-1,1,1}->List 3
S-Grph1 DrawOn,xyLine,List1,List2,1,Dot
0->A~C
Do
"A"?->A
"B"?->B
"C"?->C
Cls
Text 1,1,"Calcul."
List 1 * cos A - List 2 * sin A ->List 4
List 1 * sin A + List 2 * cos A ->List 2
List 4->List 1
Text 1,30,"."
List 2 * cos B - List 3 * sin B ->List 4
List 2 * sin B + List 3 * cos B ->List 3
List 4->List 2
Text 1,34,"."
List 1 * cos C - List 3 * sin C ->List 4
List 1 * sin C + List 3 * cos C ->List 3
List 4->List 1
Cls
Drawstat[DISP]
Lpwhile 1=1
Discutez de ce tutoriel sur le forum >> Voir le sujet dédié (121 commentaires)
|
|
Graph 35 à 100
