[Tutoriel] La 3D
Posté le 02/01/2006 13:12
Tout programmeur en basic se pose la question de la "3D" ...qui sonne si mystérieusement et délicieusement à l'oreille de tout accro du monde virtuel.
Je propose ici une approche d'une methode de rendu d'objets en 3D. Si vous etes un programmeur courageux et ambitieux passez votre chemin, regardez mes progs Util 3D et graph 3D sans regarder le code et cherchez vous meme

Je vais enployer la méthode du drawstat, pensez à regarder le tutorial dédié à cette technique si vous n'etes pas au point :).
On va travailler sur un objet simple : un cube de 2 unités de coté centré sur l'origine.
Entrons ses coordonnées :
{1,1,-1,-1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,1}->List 1
{-1,1,1,-1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1}->List 2
{-1,-1,-1,-1,-1,1,1,-1,1,1,-1,1,1,-1,1,1}->List 3
Notez que pour avoir un beau cube avec tous ses aretes en drawstat il faut repasser par certains pouints d'ou le nombre de points.
Ici List 1 = X List 2 = Y et List 3 = Z
Nous allons partir du principe que pour afficher le cube en 3D il suffit de retenir ses coordonnées en X et Y. Donc essayons d'afficher notre cube :
//paramétrez le s-graph 1 pour le drawstat en xyLine et Dot
S-WindMan // pour que nous puissions imposer la fenetre
View-Window -4,4,0,-2,2,0 // on peux prendre cette fenetre pour l'exemple car avec le coté du cube est de longueur 2
Drawstat
Et là on obtient :

On dirait un carré et pas un cube car on n'a pas ajouté d'effet de fuite. On fera ça plus tard, pour le moment on va faire tourner le cube sur lui meme

On a les coordonnées cartésiennes des points du cube mais on va utiliser les coordonnées polaires pour la démonstration de la formule que j'ai utilisé qui est sans doute la plus rapide et la plus simple.
On va faire tourner le cube selon le plan x-y puis y-z puis x-z donc en fait à chaque fois on est ramené à une rotation simple dans un plan tel que vous en connaissez depuis la seconde (au moins).
Regardez l'image suivante pour mieux comprendre ce qui suit :
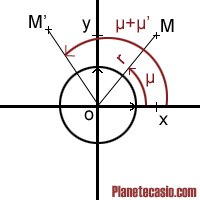
Le point initial M fait un angle µ avec l'axe des abscisses et est à une distance r de O.
M' le point image apres la rotation est également à une distance r mais fait un angle µ+µ' avec l'axe des abscisses où µ' est l'angle de rotation.
On donc en coordonnées polaires : M(r;µ) M'(r,µ+µ') et en coordonnées cartésiennes M(x,y) et M'(x',y')
On a :
x = r*cos µ x' = r*cos (µ+µ')
y = r*sin µ y' = r*sin (µ+µ')
J'imagine que vous connaissez tous tres bien vos formules de trigo donc je ne vous rappelle pas que
cos (a+b) = cos a*cos b - sin a*sin b
sin (a+b) = sin a*cos b + sin b*cos a
D'où
x' = r*cos µ*cos µ' - r*sin µ*sin µ'
= x*cos µ' - y*sin µ'
y' = r*sin µ*cos µ' + r*sin µ' *cos µ
= y*cos µ' + x*sin µ'
Et voila ! on a une magnifique formule en fonction de x, y et µ' l'angle de rotation!!!!
Simple et extremement rapide! car il suffit de 2 calculs par rotation!
J'ai mis beaucoup beaucoup de temps pour trouver ceci meme si la formule parait simple une fois ecrite il faut y penser...
Voila, je ne vous fais pas le code, je vous laisse gratter un peu quand meme

et au passage vous venez de lire en 2 min ce que j'ai cherché pendant des mois...1 an je pense :(.... (car MOI je voulais faire tout seul

)
Code d'exemple :
ClrGraph
{1,1,-1,-1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,1}->List 1
{-1,1,1,-1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1}->List 2
{-1,-1,-1,-1,-1,1,1,-1,1,1,-1,1,1,-1,1,1}->List 3
S-Grph1 DrawOn,xyLine,List1,List2,1,Dot
0->A~C
Do
"A"?->A
"B"?->B
"C"?->C
Cls
Text 1,1,"Calcul."
List 1 * cos A - List 2 * sin A ->List 4
List 1 * sin A + List 2 * cos A ->List 2
List 4->List 1
Text 1,30,"."
List 2 * cos B - List 3 * sin B ->List 4
List 2 * sin B + List 3 * cos B ->List 3
List 4->List 2
Text 1,34,"."
List 1 * cos C - List 3 * sin C ->List 4
List 1 * sin C + List 3 * cos C ->List 3
List 4->List 1
Cls
Drawstat[DISP]
Lpwhile 1=1





 et au passage vous venez de lire en 2 min ce que j'ai cherché pendant des mois...1 an je pense :(.... (car MOI je voulais faire tout seul
et au passage vous venez de lire en 2 min ce que j'ai cherché pendant des mois...1 an je pense :(.... (car MOI je voulais faire tout seul  )
)
Citer : Posté le 22/02/2014 20:01 | #
Dans un triangle ABC rectangle en A: cos ABC= AB/BC (attention, c'est l'angle ABC)
AB: côté adjacent, BC: hypoténuse
Après ça c'est le truc basique, on ne voit le cercle trigonométrique qu'en 3ème et encore, c'est pas grand chose, ça devient intéressant en 1ère
Citer : Posté le 22/02/2014 20:23 | #
...ça devient intéressent ...
"intéressant",la fatigue...
Aussi le signe * sert à quoi je ne l'ai pas trouvé dans la liste des fonctions basic casio.
-ASM (assembleur) sur x86 et gb-Z80
-locomotive basic/amstrad basic
-Basic Casio
-VBS
-Batch
-Bash
-Python 3.4
-html
-CSS
-javascript
-Lua
-brainfuck
-ruby
Il faut savoir que je ne maitrise pas parfaitement tout ces langages
[/spoiler]
Remerciment
Ma calto: graph 75
Citer : Posté le 22/02/2014 20:24 | #
Je pense que c'est une multiplication
Citer : Posté le 22/02/2014 20:29 | #
Alors pourquoi ne pas mettre × tout simplement :huh:
-ASM (assembleur) sur x86 et gb-Z80
-locomotive basic/amstrad basic
-Basic Casio
-VBS
-Batch
-Bash
-Python 3.4
-html
-CSS
-javascript
-Lua
-brainfuck
-ruby
Il faut savoir que je ne maitrise pas parfaitement tout ces langages
[/spoiler]
Remerciment
Ma calto: graph 75
Citer : Posté le 22/02/2014 20:30 | #
Le * est plus souvent utilisé dans les autres langages, mais en basic casio c'est x, mais ça ne change pas grand chose
Citer : Posté le 22/02/2014 20:30 | #
PS:c'est peut être plus rapide.
Ajouté le 22/02/2014 à 20:35 :
J'ai pas eu le temps de lire,j'ai rien dit
-ASM (assembleur) sur x86 et gb-Z80
-locomotive basic/amstrad basic
-Basic Casio
-VBS
-Batch
-Bash
-Python 3.4
-html
-CSS
-javascript
-Lua
-brainfuck
-ruby
Il faut savoir que je ne maitrise pas parfaitement tout ces langages
[/spoiler]
Remerciment
Ma calto: graph 75
Citer : Posté le 06/02/2015 14:44 | #
Comment on fait pour ceux qui sont en troisieme comme moi et qui ne connaisse pas encore les angles d'Euler (Merci Muelsaco), et autre truc que l'on ne connait pas en 3°?
Merci d'avance.
PM Générateur
graph100+ bleue
Neuronix9302
2nde GT
Citer : Posté le 06/02/2015 14:44 | #
On attend
Citer : Posté le 06/02/2015 15:28 | #
Plus haut Dark Storm a linké un tuto sur la trigo.
Plus tu avanceras des tes études (en S particulièrement), plus tu utiliseras régulièrement la trigo... c'est vraiment un outil très utile.
Citer : Posté le 19/05/2016 19:58 | #
Yay
Et je vais étudier un peux la chose en C
Citer : Posté le 19/05/2016 20:08 | #
Y avait-il un effet de perspective ?
Quoiqu'il en soit si tu veux faire de la 3D puissante, tu vas utiliser aussi pas mal de transformations matricielles. Tant que tu n'utiliseras pas une base mathématique solide, je peux te garantir (par expérience) que ça restera du "bricolage" mal optimisé
Citer : Posté le 19/05/2016 20:20 | #
Hum la perspective j'ai pas essayé parce que le soucis c'est le calcul de coordonnées avec des listes, donc du calcul avec la totalité des listes de coordonnées, soit, on ne peut pas gérer les faces séparément, pour garder la vitesse de l'affichage du super drawstat
Donc je vais me pencher un peut plus sur la perspective prochainement
Hehe j'suis en spé math
En réfléchissant un peu j'ai trouvé les matrices de rotations tridimensionnelles
Puis j'ai seulement traduis les calculs pour faire du calcul sur liste
Par exemple la matrice R de rotation sur le plan (xOy)
( cos a -sin a 0 )
( sin a cos a 0 )
( 0 0 1 )
Les coordonnées de A en matrice
( x )
( y )
( z )
Puis pour faire tourner A autour d'un point O (imaginer des coordonnées en matrice comme A) :
A' = R (A - O) + O
Citer : Posté le 19/05/2016 20:36 | #
Ouaip, c'est exactement celles-là
J'ai implémenté ça il y a quelques temps sur mon PC, mais j'arrive pas à appliquer des perspectives satisfaisantes... je ne sais pas trop si ça peut se calculer avec des matrices, j'ai des doutes sur la linéarité de la perspective.
Enfin après une fois que t'as la matrice de rotation c'est fini, quelques calculs matriciels te permettront d'afficher un monde en 3D dans toutes les directions. La perspective reste le dernier élément en général...
Citer : Posté le 19/05/2016 20:41 | #
Merci
Je check les fonctions Basic du style Mat→List pour voir si je peux revenir à mon calcul matriciel, et stocker toutes les "faces" de mon cubes dans une matrice pour pouvoir les extraire et les traiter séparément
En soit la perspective c'est juste décaler chaque point dans le sens opposé de l'origine de ta caméra en fonction de leur profondeur
Citer : Posté le 19/05/2016 20:45 | #
Nan, la perspective c'est plus difficile que ça. Tu peux essayer, tu verras vite...
Par contre si tu veux faire un truc efficace il va falloir rapidement quitter le Basic
Citer : Posté le 19/05/2016 20:47 | #
Hum Ah mince
Ouaip, je m'attellerais à ça en C après le Bac
Ajouté le 19/05/2016 à 21:31 :
Bon, à coup de "Trn Mat A" de "Mat X→Mat R" etc... J'ai réussi à transformer ce calcul de list, en calcul matriciel, et devinez quoi
J'ai seulement perdu 0.2 secondes
Maintenant j'attaque la "découpe" des faces
Citer : Posté le 09/01/2017 16:06 | #
Tu n'as pas à gérer les faces indépendament les unes des autres. D'autant plus pour la perspective cela n'a pas de sens... Ajouter la perspective est simple en vérité. Si tu as un point aux coordonnées (x; y; z), les coordonnées projetées sur l'écran sont (x/z; y/z). Donc pas de calcul listique trivial ici, sinon la perspective peut aussi être calculée avec les matrices, mais on passe, gentillement, en 4 dimension
Voilà comment doit s'organiser un petit moteur 3D :
- Avoir les coordonnées des points d'un objet dans le repère monde.
- Transformer ces coordonnées vers le repère caméra (rotation, translation)
- Transformer ces coordonnées vers le repère de l'écran (perspective)
- Affichage (relier les points par exemple)
Si tu veux afficher un cube, tu peux gérer intelligemment l'oclusion des faces en regardant le signe du produit scalaire entre la normal à ta face et l'axe de la caméra.
Je parle d'experience
Citer : Posté le 06/09/2018 09:12 | #
Cool
Citer : Posté le 06/09/2018 12:49 | #
Sinon je m'y suis moi même intéressé sur mon topic: http://www.planet-casio.com/Fr/forums/topic14655-1-Les_espaces_3D_(coder).html
Ajouté le 06/09/2018 à 12:49 :
Tu y trouveras peut être des détails supplémentaires
-Planétarium 2