Physique d'un grappin
Posté le 09/01/2022 10:59
yow
En ce moment pour un petit projet d'add-in, j'ai besoin de développer un grappin.
Il pourra s'accrocher à des points fixes définis et permettra au joueur de s'élancer et/ou de prendre de la hauteur. N'ayant pas fait spécialité physique/chimie, je me retrouve dans le flou total quand il s'agit de programmer ce truc.
Cette mécanique est directement volée d'un
demake PICO-8 de A Hat in Time (la mécanique rend très très bien). J'ai essayé de reprendre le code écrit en Lua afin de l'appliquer sur mon jeu, mais que ce soit sur un proto avec LÖVE ou bien en C sur mon jeu, ça donne un résultat catastrophique (en C, le personnage part même de manière incontrôlée par moment).
Voici le bout de code en question :
function move_hook(v)
-- Note : v représente le hook, p1 le joueur
-- p1.dx et p1.dy contiennent la vitesse du joueur
-- measure hyp between hook and
-- hat kid
i = abs(v.x-p1.x)
j = abs(v.y-p1.y)
k = sqrt(i*i + j*j) -- calcul de la distance
v.k = k
if k < 40 and
v.y-p1.y < 0 then
v.range = true
else
v.range = false
end
-- if hyp is short enough, set
-- latched to true
if btn(5) and
v.range == true then
v.latch = true
else
v.latch = false
end
-- latch behavior
if v.latch == true then
-- pull hat kid toward latch
-- distance sur les axes x et y entre le joueur et le crochet
i = v.x-p1.x
j = v.y-p1.y
-- ramène le joueur vers le crochet
if abs(p1.dy)<5 then
p1.dy += j*(1.2/k)
end
if abs(p1.dx)<5 then
p1.dx += i*(.5/k)
end
end
end
Comme j'ai du mal à l'expliquer, voici un schéma :
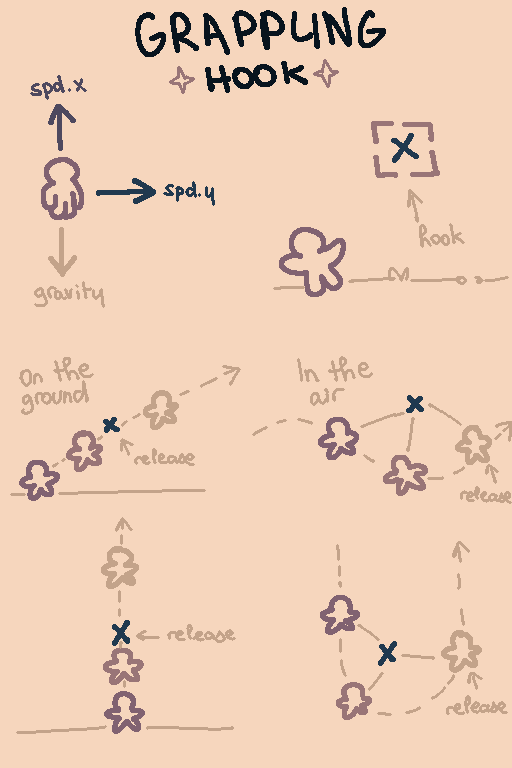
Le grappin doit être en mesure de propulser le joueur lorsqu'il est au sol , mais aussi le balancer lorsqu'il est dans les airs. Je me demande si les deux comportements sont compatibles d'un point de vue physique, étant donné qu'il y en a qui demande le rétrecissement de la corde et l'autre de conserver une longueur égale x)
Quelqu'un aurait-il des pistes ou formules pour m'éclairer ?
Merci beaucoup

 Fichier joint
Fichier joint



Citer : Posté le 09/01/2022 11:10 | #
Je m'attends à ce que Kouhai ou quelqu'un d'autre donne plein de détails, alors juste une remarque rapide :
Le fait que le grappin puisse te tirer est indépendant du fait que tu puisses te balancer avec.
Citer : Posté le 09/01/2022 11:11 | #
C'est de la mécanique toute bête
Pour certains il faudrait que je fasse des calculs en prenant une masse pour le joueur, pour le cas en bas à droite, l'angle θ est une fonction du temps et vérifie l'équa diff :
d²θ/dt² + g/l sin θ = 0 (avec l la longeur de la corde)
Je t'épargne les détails, mais si je me souviens bien, θ(t) = v / sqrt(g / l) × sin(sqrt(g/l) t) avec l la longueur de ta corde. (Lephe ou Alice pour confirmer, je suis pas contre xD)
Citer : Posté le 09/01/2022 11:14 | #
Je suis à peu près sûr que si tu t'accroches à un moment où ta vitesse est tangente tu fais un arc de cercle... à vérifier du coup, tu me mets le doute.
Citer : Posté le 09/01/2022 11:23 | #
Ce serait juste un sinus du temps alors ?
Pour le cas en bas à gauche, c'est assez simple, tant que ton personnage monte tu peux juste augmenter sa vitesse de déplacement vers le haut selon une exponentielle (c'est pas de la méca là) genre x_max (1 - exp(-t/X)) avec X une constante positive. Tu peux prendre une loi linéaire aussi.
Si ton personnage à une masse m, on a
sa vitesse : v = -mg⋅t + v0 où v0 est la vitesse au moment du lâcher
sa position : x = -mg⋅t² + v0⋅t + x0 où x0 est la position au moment du lâcher
Citer : Posté le 09/01/2022 11:24 | #
je crois ca a quelque chose a voir avec le momentum, je ne connais que le mot et vaguement le concept, je t'invite a continuer ta recherche par toi meme (la force de gravite est limitee par le fil et donc toute cette force devient une force sur l'axe x et non y je crois)
apres le cours de physique le plus avance que j'ai fait c'est un cours sur le mouvement, donc je ne suis pas une source vraiment credible
Citer : Posté le 09/01/2022 11:30 | #
Lephé : pour le grappin et le personnage qui tourne autour du point d'accorche, ça peut pas être juste un arc de cercle, la gravité va tendre à faire osciller le personnage autour de la seule position d'équilibre stable, donc c'est bien une équa diff (sans doute d'ordre 1 car on va dire que les frottements, osef
Citer : Posté le 09/01/2022 11:32 | #
On oscille oui... sur un arc de cercle. Je vois pas trop comment ça pourrait être une parabole vu que la corde est toujours tendue ; la distance entre le point d'accroche et la position du joueur est donc forcément une constante.
Je suis d'accord cela dit qu'une formulation en équa diffs est supérieure, comme ça t'as juste à intégrer par simulation et en termes de code c'est trivial. C'est un peu ce qui se passe dans le code Lua d'ailleurs, si mes yeux ne me trompent pas.
Citer : Posté le 09/01/2022 11:34 | #
Ah si la longueur est constante, oui ça doit faire un arc de cercle
Citer : Posté le 09/01/2022 11:38 | #
quand le joueur est au dessus du sommet du fil c'est une droite qui va vers le bas non?
Citer : Posté le 09/01/2022 11:50 | #
@Gladosse : j'ai pas tout compris… le joueur ne peut pas rester au dessus de son point d'accroche, la gravité va tendre à le ramener vers le bas. Note que si le fil avait été une tige, ça aurait été possible, mais c'est une position d'équilibre instable (un toute petite variation suffit à faire repartir le pendule vers une position d'équilibre stable)
Pour le cas du grappin qui tire le joueur selon une ligne oblique, si je me suis pas planté, on a :
sa vitesse selon l'axe des x : -gt + v0x sin α
sa vitesse selon l'axe des y : v0y⋅cos α
sa position selon l'axe des x : -gt²/2 + v0⋅t⋅sin α + x0x
sa position selon l'axe des y : v0⋅t⋅cos α + x0y
En notant :
α l'angle entre l'axe des y et le segment qui représente le fil du grappin
v0x, v0y les composantes selon x et y du vecteur vitesse à l'instant initial (au moment où le joueur relâche le grappin)
x0x, x0y idem mais pour la position
Ajouté le 09/01/2022 à 11:57 :
Pour le cas en haut à droite, c'est un mélange entre les cas précédents :
- La petite parabole que tu as dessiné, correspond à une équation du second degré (cf. mon message précédent)
- L'arc de cercle parcouru par le joueur est donné par une équation différentielle, d²θ/dt² + g/l sinθ = 0 avec θ l'angle que le fil forme avec l'axe des x.
Ajouté le 09/01/2022 à 12:07 :
Bon, je crois que j'ai trouvé, c'est pas très joli comme expression, mais si je me suis pas planté,
la vitesse angulaire dθ/dt a pour expression :
dθ/dt (t) = -θ0⋅w0⋅sin(w0⋅t) + v0⋅cos(w0⋅t)
et l'angle θ a pour expression :
θ(t) = θ0⋅cos(w0⋅t) + (v0 / w0)⋅sin(w0⋅t)
Avec v0 la vitesse au moment où le grappin s'accroche
θ0 l'angle entre l'axe des x et le fil du grappin au moment où le grappin s'accroche
w0, (la pulsation caractéristique) qui a pour expression : sqtr(g / l) avec g la gravité, et l la longueur du fil
Je suis contre une vérification, mais je crois que c'est correct
Citer : Posté le 09/01/2022 13:04 | #
Je vais être franc : J'ai pas réussir à suivre tes explications Shadow
Du coup il faudrait avoir deux comportements différents, un pour le propulsage et l'autre pour le balancement ?
Et les ⋅ c'est une multiplication ou un produit scalaire ?
Citer : Posté le 09/01/2022 13:09 | #
Salut Massena,
Les équations de Shadows sont sans doute correctes, mais tu ne pourras pas les exploiter pour ton jeu.
L'approche par équation exact ne me semble pas la bonne approche.
Après avoir joué au jeu quelques minutes, pense que la mécanique est très simple
player.acceleration += player_hook * coef // on modifie l'acceleration du joueur
si (player.acceleration > acceleration_max) player.acceleration = acceleration_max // on bride l'acceleration
Citer : Posté le 09/01/2022 13:21 | #
Je pense que oui ^^' Après l'idée de Ninestars me paraît bien, tu n'as peut-être pas besoin des équations du mouvements exacte.
Désolé pour la notation foireuse ^^' c'est bien une multiplication (note que la multiplication usuelle est un produit scalaire, donc l'un dans l'autre… bon voila xD)
Ces équations permettent de trouver les vecteurs vitesse et la position du joueur à tout instant, je pense que ça peut être implémenter et même plutôt bien fonctionner
Citer : Posté le 09/01/2022 14:25 | # | Fichier joint
Fichier joint
Je met en fichier joint un doc avec les équations de la position et de la vitesse du joueur dans les différents cas de figure.
Citer : Posté le 09/01/2022 15:15 | #
Merci beaucoup, ça marche beaucoup mieux ! Désolé Shadow si tu t'es embêté à faire un PDF pour rien, mais la méthode de Ninestars était beaucoup plus simple et accessible à mon niveau
Voici le code pour les interessés :
player_hook(void)
{
struct Vec2 player_middle = {player.pos.x + PLAYER_S / 2,
player.pos.y + PLAYER_S / 2};
/* get the nearest hook */
if (!player.locked) {
player.hook_pos = hook_closest(&player_middle);
}
const float dist = length(player_middle.x, player_middle.y,
player.hook_pos.x, player.hook_pos.y);
/* if the nearest hook is in range */
if (dist < 100 && player_middle.y > player.hook_pos.y) {
player.hooking = 1;
player.locked = 1;
player.jumping = 1;
}
if (player.hooking && dist) {
/* determining hook force */
float dist_x = player.hook_pos.x - player_middle.x;
float dist_y = player.hook_pos.y - player_middle.y;
struct FVec2 force = {};
if (dist_x) {
force.x = dist_x / dist;
}
if (dist_y) {
force.y = dist_y / dist;
}
/* apply hook force */
player.spd.x += force.x;
player.spd.y += force.y;
/* cap speed */
if (abs(player.spd.x) > 16) {
player.spd.x = 8 * sign(player.spd.x);
}
if (abs(player.spd.y) > 8) {
player.spd.y = 8 * sign(player.spd.y);
}
}
}
Citer : Posté le 09/01/2022 15:16 | #
Y a aucun problème, ça m'a fait réviser ma méca.
Citer : Posté le 09/01/2022 16:25 | #
Avec plaisir
Au passage, dans ton code tu peux retirer les conditions pour éviter les divisions:
if (dist_x) et if (dist_y)
car 99 fois sur 100 ta force sera sur deux dimensions.
T'as peut être une erreur sur le player.spd.x = 8 * sign(player.spd.x); ? Ce ne serait pas un 16 plutôt ?
Citer : Posté le 09/01/2022 16:30 | #
Bien vu pour les deux, c'est corrigé. Merci