Rendu graphique en Python, Partie 1 - Découverte de Matplotlib et Turtle
Posté le 07/04/2020 18:19
Bonjour à toi, visiteur de ce forum. Casio vient de publier sa mise à jour Python incluant les modules matplotl et turtle pour Graph 35+E II et Graph 90+E. Alors voyons ce que ça donne en vrai ! 
Les modules avaient été
annoncés dans la dernière newsletter de Casio en Février, et les exemples proposés démontraient une
compatibilité totale entre calculatrice et PC sur les fonctions simples des deux modules. On se félicite d'avoir accès à des modules cross-platform qui faciliteront grandement le travail des professeurs et des élèves. Notons que Numworks a fait le même choix avec des bons résultats. Voyez les
tests de Critor sur ce point.

La mise à jour est désormais en ligne et porte un nouveau numéro de version de l'OS. La version supportant les modules matplotl et turtle est :
• La
version 3.30 sur Graph 35+E II,
• La
version 3.40 sur Graph 90+E.
La mise à jour est
disponible en ligne sur le site de Casio et consiste, comme d'habitude, en un fichier exécutable permettant d'installer le nouvel OS sur ta calculatrice. Mais cette fois, ce n'est pas tout ! Il y a aussi deux scripts
matplotl.py et
turtle.py qui vont avec et qui sont téléchargeables
dans la section ressources du site Casio Éducation. Il faut un compte pour y accéder, alors à la place vous pouvez aussi les télécharger
directement sur cette page (archive zip).
Mais alors, si l'OS n'intègre pas directement matplotlib et turtle, pourrait-il contenir d'autres fonctions utiles pour développer des jeux ? 
Nous allons voir tout ça ensemble. J'ai installé les modules sur ma Graph 90+E et ma Graph 35+E II, c'est le moment de jouer avec ! Je vais montrer des images de la Graph 35+E II parce qu'elle est beaucoup plus pratique pour faire des captures, mais ce que je raconte concerne les deux modèles.
Changements depuis la version précédente
La Graph 35+E II affiche désormais le message "Des extensions supprimées par Réinitialisation1 sont installées". Ce message a été ajouté sur la Graph 90+E il y a un moment et signifie en gros que les add-ins sont désactivés en mode examen. Rien d'inattendu ici !

La Graph 35+E II est désormais en OS 3.30 et contient les deux scripts
matplot.py et
turtle.py une fois qu'ils ont été transférés. Pareil pour la Graph 90+E dont l'OS est maintenant appelé 3.40.
Attention à ne pas confondre l'OS 3.30 de la Graph 35+E II et l'OS 3.30 de la Graph 90+E !

 Exemples standard de matplotlib et turtle
Exemples standard de matplotlib et turtle
Regardons un exemple présenté sur la Graph 90+E dans la newsletter, mais sur la Graph 35+E II : celui de l'histogramme.
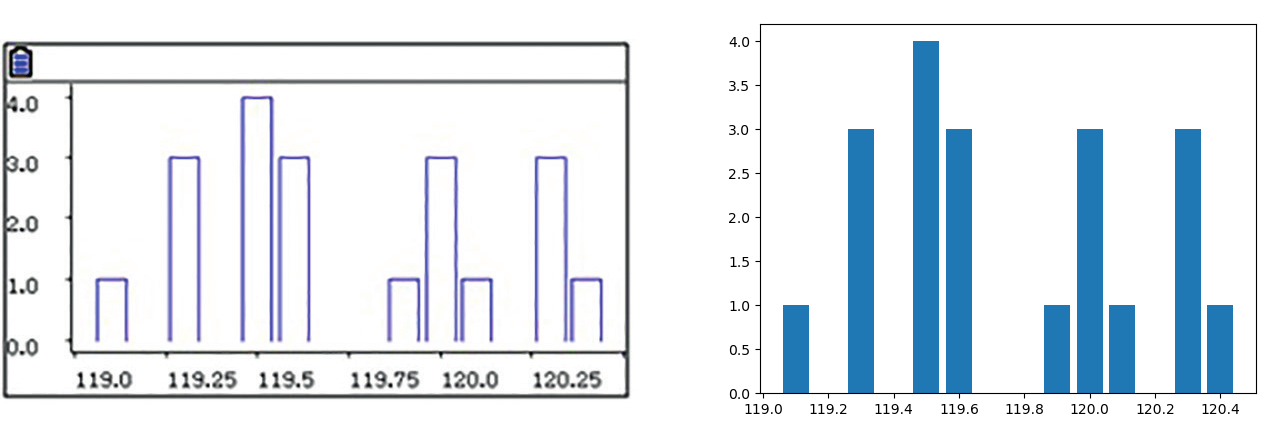
Voici le code et ce que ça donne sur la calculatrice :
import matplotl as p
x=[119.1,119.3,119.5,119.6,119.9,120.0,120.1,120.3,120.4]
y=[1,3,4,3,1,3,1,3,1]
p.bar(x,y,0.08)
p.show()

C'est un peu serré... mais pas si mal ! Les labels de l'axes des abscisses ne font pas de cadeau, ils sont à la fois longs et nombreux sur cet exemple.

Cet exemple met longtemps à s'exécuter. Pas loin de 9 secondes, ce qui est... normal ! Eh oui, il faut charger
matplot.py en entier, et c'est un script de 40000 caractères. C'est de loin ce qui prend le plus longtemps (pour le voir on peut mettre deux listes
x et
y de taille différente, et l'erreur met longtemps à arriver).

Voyons voir ce qui se passe du côté de turtle. J'ai codé le même script de flocon de Koch que présenté avant.
from turtle import *
def koch(n,l):
if n==0:
forward(l)
else:
koch(n-1,l/3)
left(60)
koch(n-1,l/3)
right(120)
koch(n-1,l/3)
left(60)
koch(n-1,l/3)
pencolor("black")
penup()
goto(-120,-10)
pendown()
koch(4,120)
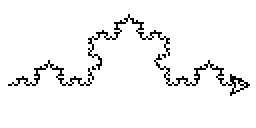
Ce script qui effectue 81 tracés de lignes et des rotations met 3 secondes à charger turtle et... presque une minute à faire le dessin ! Mais là encore ça ne condamne pas les performances, car...

• turtle rafraîchit l'écran à chaque ligne, ce qui gâche des ressources (on en reparlera).
• turtle redessine la tortue à chaque ligne, ce qui est plus long que de tracer la ligne (!)
• Et surtout turtle fait beaucoup de calculs trigonométriques car la tortue fonctionne sur un système d'angles.
Alors voyons ce qui se cache derrière ses modules de dessin et ce que les performances sont vraiment.
 La vraie bibliothèque de dessin en Python, casioplot
La vraie bibliothèque de dessin en Python, casioplot
Comme annoncé dans la newsletter, les modules
matplotl et
turtle reposent sur un module de dessin spécifique appelé
casioplot. C'est lui qui est inclus dans la mise à jour de l'OS !
Que contient ce module ? Pour le savoir, il suffit de lire
matplotl.py et
turtle.py. C'est ce que j'ai fait pour vous. Voici le verdict !
casioplot est un module de dessin bas-niveau qui écrit très certainement directement dans la VRAM. Il permet de dessiner à l'écran avec des positions en pixels. Les fonctions sont les suivantes :
•
casioplot.clear_screen()
•
casioplot.set_pixel(x,y,(R,G,B))
•
casioplot.get_pixel(x,y)
•
casioplot.draw_string(x,y,text,(R,G,B),size)
•
casioplot.show_screen()
Ce sont les fonctions de base que l'on pouvait attendre. Il n'y a pas de tracé de ligne ou de cercle, car matplotl et turtle le recodent. Les lignes sont tracées avec l'algorithme de Bresenham, les cercles avec... de la trigo ! (Ce qui est une très mauvaise idée car c'est extrêmement lent, des vrais algorithmes comme
celui du point médian sont faits pour ça.)
Pour dessiner, on a donc
set_pixel() et
draw_string(), qui peut utiliser à la fois la petite police et la grande ! On peut lire la couleur des pixels à l'écran avec
get_pixel(), ce qui est un ajout assez cool ! Les couleurs sont en RGB avec chaque composante entre 0 et 255. C'est le cas également sur la Graph 35+E II, les couleurs sont justes approximées par du noir et blanc selon ce qui est le plus proche.
L'existence de
casioplot.show_screen() est très importante ! Contrairement au Basic, les dessins tracés avec casioplot ne sont pas affichés immédiatement. Cette technique s'appelle le
double buffering et a plusieurs avantages :
• Ça évite que l'utilisateur voie un dessin inachevé, car tu peux n'appeler
show_screen() qu'une fois le dessin fini.
• C'est beaucoup plus rapide car dessiner va souvent bien plus vite qu'afficher à l'écran, et donc on évite beaucoup de travail en plus.
Voici un petit programme pour donner le ton.
from casioplot import *
B=(0,0,0)
W=(255,255,255)
clear_screen()
set_pixel(1, 1, B)
for x in range(10):
set_pixel(x+1,3,B)
for y in range(40):
for x in range(10):
set_pixel(x+1,y+5,B)
draw_string(20,1,"Hello,",B,"large")
draw_string(20,11,"World!",B,"small")
img = b'\x04@"\x00\x0e\xa6W\x00\x0e\xafW\x00\x05\x1f\x89\x00u/J\xc0\xf5F*\xe0'+\
b'\xe4\xc92\xe0\x8cP\xa1 \x8c{\xe1 \x8c\xbf\xb1 \x8c\xb1\xb1 \x9c\x950'+\
b'\xa0\x9e\xb1\x90\xa0\x8e\x7f\xc3 \xc3\xfb\xfc`\xe0\x1d\xc0\xe0\xbf\x12'+\
b'\x1f\xa0_\t\x1f@ \x89 \x80\x1f\x92?\x00'
for y in range(20):
for x in range(27):
offset = y * 4 + (x // 8)
bit = 0x80 >> (x & 7)
if img[offset] & bit:
set_pixel(x+30,y+30,B)
show_screen()
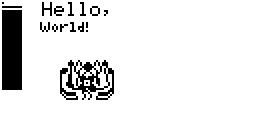
Boum! Moins d'une demi-seconde pour importer le module, faire le tracé, et mettre à jour l'écran. C'est
de très, très loin plus rapide que le Basic Casio pour le dessin ! Comme on l'avait soupçonné, les performances réduites de matplotl et turtle ne sont pas à cause du dessin pur, ce qui ouvre beaucoup de possibilités pour des programmes plus ludiques !

Pour ceux qui se demandent, les caractères bizarres au milieu du script sont un encodage bitmap de l'image du château, qui vient de
SwordBurstZero.

Il y a beaucoup, beaucoup plus de choses à dire sur ces bibliothèques. On va s'arrêter là pour aujourd'hui mais on prendra bien sûr le temps d'y revenir !
 À venir dans les prochains articles
À venir dans les prochains articles
Dans la suite, on regardera quelles sont les différences entre les versions Graph 35+E II et Graph 90+E de matplotlib, turtle et casioplot.
On s'intéressera aussi aux performances plus en détail, avec des exemples plus simples pour tester si le tracé, le dessin ou l'exécution du Python sont les facteurs limitants. Si vous avez déjà essayé chez vous, partagez vos résultats dans les commentaires !

Enfin, on organisera un petit concours consistant à programmer des
démos (petits programmes graphiques qui tournent généralement en boucle et affichent des dessins ou animations rigolos) avec ces modules, pour voir jusqu'où vous pouvez abuser de ces nouvelles fonctionnalités.
 À bientôt sur Planète Casio !
À bientôt sur Planète Casio !  Liens de téléchargement :
Liens de téléchargement :
•
Téléchargement de la mise à jour
•
Scripts matplotl.py et turtle.py pour Graph 35+E II et Graph 90+E
•
Section ressources de Casio Éducation
 Fichier joint
Fichier joint












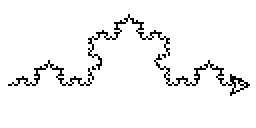


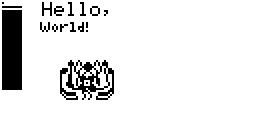






Citer : Posté le 08/04/2020 11:53 | #
Voilà désolé, toujours dans des conditions informatiques très précaires suite à une panne d'ordi hélas des plus graves lundi matin, mais j'ai pu mettre en avant cette fantastique mise à jour et rajouter la référence, enfin :
https://tiplanet.org/forum/viewtopic.php?p=252337#p252337
Quel dommage que turtle.py et matplotl.py ne marchent pas en mode examen, c'est hélas également un gros défaut pour la France.
Citer : Posté le 08/04/2020 12:23 | #
Et un point pour la Numworks
-Planétarium 2
Citer : Posté le 09/04/2020 19:51 | #
Au passage, j'ai fais quelques tests, et si on se base sur get_pixel(x, y) qui retourne None lorsque le pixel est hors de la zone de dessin, on tombe sur une zone utilisable de 384×192 pixels sur la G90+E
Ça vaut peut être le coup de l'ajouter dans l'article
Citer : Posté le 09/04/2020 20:20 | #
Merci. J'avais vu et mis dans mon article de mon côté. De quoi retrouver les valeurs facilement plutôt que d'avoir à les retenir par cœur :
def getScreen():
w, h = 0, 0
while(scr.get_pixel(w, 0)):
w += 1
while(scr.get_pixel(0, h)):
h += 1
return (w, h)
Mais pour un script destiné à tourner sur différents modèles pour un concours de rentrée ou autre, il faut savoir que cette astuce formidable ne marche apparemment pas sur NumWorks.
Citer : Posté le 09/04/2020 20:55 | #
Au passage Critor, je soupçonne une erreur dans ton article : écrire (1,1,1) et tester si on lit (0,0,0) ne marche pas je pense parce que l'écran de la Graph 90+E est en R5G5B6 et donc (1,1,1) est assimilé à (0,0,0) là aussi. Il faudrait mettre un truc un peu plus gros
Citer : Posté le 09/04/2020 21:23 | #
Oui merci beaucoup à toi.
Je m'en étais déjà douté à la lecture de plusieurs infos ici.
Mais dans ma situation informatique actuelle bien compliquée depuis lundi matin, je n'ai pas encore fait l'effort de corriger ce passage...
Citer : Posté le 09/04/2020 22:15 | # | Fichier joint
Fichier joint
Une ptite démo, qui utilise un bout de lib créé pour l'occasion
from casioplot import clear_screen, show_screen, set_pixel
color=HSL(0,1.0,1.0)
clear_screen()
for x in range(384):
color.h=x*360/384
for y in range(192):
color.l=y/192
set_pixel(x,y,color.rgb().raw())
show_screen()
Citer : Posté le 09/04/2020 22:44 | #
c=v*s
x,m,k=c*(1-abs((h%(2/3))*3-1)),v-c,(h*3)//1
return (round(255*(m+x*(k%3==1)+c*(k%5==0))),round(255*(m+c*(k==1 or k==2)+x*(k%3==0))),round(255*(m+x*(k%3==2)+c*(k==3 or k==4))))
Citer : Posté le 10/04/2020 08:24 | # | Fichier joint
Fichier joint
J'ai adapté un raytracer que j'avais fait en python, cependant il fait 13ko, ce qui l'empêche d'être éditable sur calto :
Citer : Posté le 10/04/2020 08:25 | # | Fichier joint
Fichier joint
cependant, voilà une image sans déformation :
Citer : Posté le 10/04/2020 08:58 | #
Trop classe !!
Citer : Posté le 10/04/2020 09:14 | #
Merci @Dark_storm d'avoir rajouté le code d'appel.
Superbe @Lightmare !
Tu nous montres ton code toi aussi ?
Citer : Posté le 10/04/2020 09:23 | # | Fichier joint
Fichier joint
Alors c'est moche et pas du tout optimisé, mais il marche !
import math
h = int(input("hauteur : "))
w = int(input("longueur : "))
pi = 3.14159265359
sphere = [0,7,1,2, 1]
plane = [0,0,-0.25,-1]
light = [2,2,10]
inter_sph = [0,0,0]
diam_vec = [0, 0, 0]
ray = [0,0,0]
light_ray = [0,0,0]
a = 0
b = 0
c = 0
cam_vec = [0,1,0,0,0]
cam_vec[3] = math.acos(cam_vec[0] / math.sqrt(2))
cam_vec[4] = math.asin(cam_vec[1] / math.sqrt(2))
cam_vec[3] += pi / 4
cam_vec[4] += pi / 4
cor_x = math.cos(cam_vec[3]) * math.sqrt(2)
cor_y = math.cos(cam_vec[4]) * math.sqrt(2)
cor_z = math.cos(cam_vec[2] / math.sqrt(2) + pi / 4) * math.sqrt(2)
ray[0] = cam_vec[0] + cor_x
ray[1] = cam_vec[1] + cor_y
ray[2] = cam_vec[2] + cor_z
for y in range(1, h) :
for x in range(1, w) :
ray[0] = x * (2/w) + cor_x
ray[2] = cor_z - y * (2/h)
delta = 4*pow(a*ray[0] + b*ray[1] + c*ray[2] - ray[0]*sphere[0] - ray[1]*sphere[1] - ray[2]*sphere[2], 2) - 4*(pow(ray[0], 2) + pow(ray[1], 2) + pow(ray[2], 2))*(-2*a*sphere[0] - 2*b*sphere[1] - 2*c*sphere[2] + pow(a,2) + pow(b,2) + pow(c,2) + pow(sphere[0],2) + pow(sphere[1],2) + pow(sphere[2],2) - pow(sphere[3],2))
if delta > 0 :
t = (-2*(a*ray[0] + b*ray[1] + c*ray[2] - ray[0]*sphere[0] - ray[1]*sphere[1] - ray[2]*sphere[2]) - math.sqrt(delta)) / 2*(pow(ray[0], 2) + pow(ray[1], 2) + pow(ray[2], 2))
if plane[0]*ray[0] + plane[1]*ray[1] + plane[2]*ray[2] != 0 :
t_2 = -(plane[0]*a + plane[1]*b + plane[2]*c + plane[3]) / (plane[0]*ray[0] + plane[1]*ray[1] + plane[2]*ray[2])
if t_2 > 0 and delta > 0 :
if t_2 > t :
inter_sph[0] = a+t*ray[0]
inter_sph[1] = b+t*ray[1]
inter_sph[2] = c+t*ray[2]
light_ray[0] = light[0] - inter_sph[0]
light_ray[1] = light[1] - inter_sph[1]
light_ray[2] = light[2] - inter_sph[2]
if sphere[4] == 0 :
delta_2 = 4*pow(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2], 2) - 4*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))*(-2*inter_sph[0]*sphere[0] - 2*inter_sph[1]*sphere[1] - 2*inter_sph[2]*sphere[2] + pow(inter_sph[0],2) + pow(inter_sph[1],2) + pow(inter_sph[2],2) + pow(sphere[0],2) + pow(sphere[1],2) + pow(sphere[2],2) - pow(sphere[3],2))
if delta_2 >= 0 :
r_1 = (-2*(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2]) - math.sqrt(delta_2)) / 2*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))
r_2 = (-2*(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2]) + math.sqrt(delta_2)) / 2*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))
if abs(r_1) > abs(r_2) :
color = (0,0,255)
else :
color = (0,0,255 - (r_2*255)/(abs(r_1)+r_2))
else :
color = (0,0,255)
else :
diam_vec[0] = inter_sph[0] - sphere[0]
diam_vec[1] = inter_sph[1] - sphere[1]
diam_vec[2] = inter_sph[2] - sphere[2]
k = (diam_vec[0]*(a - sphere[0]) + diam_vec[1]*(b - sphere[1]) + diam_vec[2]*(c - sphere[2])) / (pow(diam_vec[0], 2) + pow(diam_vec[1], 2) + pow(diam_vec[2], 2))
l = (pow(diam_vec[0], 2) + pow(diam_vec[1], 2) + pow(diam_vec[2], 2))*pow(k, 2) + 2*(diam_vec[0]*(a - sphere[0]) + diam_vec[1]*(b - sphere[1]) + diam_vec[2]*(c - sphere[2])) + (pow(sphere[0] - a, 2) + pow(sphere[1] - b, 2) + pow(sphere[2] - c, 2))
proj = [k*diam_vec[0] + sphere[0] , k*diam_vec[1] + sphere[1] , k*diam_vec[2] + sphere[2]]
refl = [2*(proj[0] - a) + a , 2*(proj[1] - b) + b , 2*(proj[2] - c) + c]
reflect = [refl[0] - inter_sph[0] , refl[1] - inter_sph[1] , refl[2] - inter_sph[2]]
if plane[0]*reflect[0] + plane[1]*reflect[1] + plane[2]*reflect[2] != 0 :
t_2 = -(plane[0]*inter_sph[0] + plane[1]*inter_sph[1] + plane[2]*inter_sph[2] + plane[3]) / (plane[0]*reflect[0] + plane[1]*reflect[1] + plane[2]*reflect[2])
if t_2 > 0 :
if (int(inter_sph[0]+t_2*reflect[0])/2 == int((inter_sph[0]+t_2*reflect[0]) / 2) and not int(inter_sph[1]+t_2*reflect[1]) / 2 == int((inter_sph[1]+t_2*reflect[1]) / 2)) or (not int(inter_sph[0]+t_2*reflect[0])/2 == int((inter_sph[0]+t_2*reflect[0]) / 2) and int(inter_sph[1]+t_2*reflect[1]) / 2 == int((inter_sph[1]+t_2*reflect[1]) / 2)):
color = (0,255,0)
else :
color = (255,0,0)
inter_sph[0] = inter_sph[0]+t_2*reflect[0]
inter_sph[1] = inter_sph[1]+t_2*reflect[1]
inter_sph[2] = inter_sph[2]+t_2*reflect[2]
light_ray[0] = light[0] - inter_sph[0]
light_ray[1] = light[1] - inter_sph[1]
light_ray[2] = light[2] - inter_sph[2]
delta_2 = 4*pow(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2], 2) - 4*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))*(-2*inter_sph[0]*sphere[0] - 2*inter_sph[1]*sphere[1] - 2*inter_sph[2]*sphere[2] + pow(inter_sph[0],2) + pow(inter_sph[1],2) + pow(inter_sph[2],2) + pow(sphere[0],2) + pow(sphere[1],2) + pow(sphere[2],2) - pow(sphere[3],2))
if delta_2 >= 0 :
if color == (255, 0, 0) :
color = (100, 0, 0)
else :
color = (0, 100, 0)
else :
color = (0, 0, 0)
else :
if (int(b+t_2*ray[1])/2 == int((b+t_2*ray[1]) / 2) and not int(a+t_2*ray[0]) / 2 == int((a+t_2*ray[0]) / 2)) or (not int(b+t_2*ray[1])/2 == int((b+t_2*ray[1]) / 2) and int(a+t_2*ray[0]) / 2 == int((a+t_2*ray[0]) / 2)):
color = (0,255,0)
else :
color = (255,0,0)
inter_sph[0] = a+t_2*ray[0]
inter_sph[1] = b+t_2*ray[1]
inter_sph[2] = c+t_2*ray[2]
light_ray[0] = light[0] - inter_sph[0]
light_ray[1] = light[1] - inter_sph[1]
light_ray[2] = light[2] - inter_sph[2]
delta_2 = 4*pow(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2], 2) - 4*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))*(-2*inter_sph[0]*sphere[0] - 2*inter_sph[1]*sphere[1] - 2*inter_sph[2]*sphere[2] + pow(inter_sph[0],2) + pow(inter_sph[1],2) + pow(inter_sph[2],2) + pow(sphere[0],2) + pow(sphere[1],2) + pow(sphere[2],2) - pow(sphere[3],2))
if delta_2 >= 0 :
if color == (255, 0, 0) :
color = (100, 0, 0)
else :
color = (0, 100, 0)
elif t_2 > 0 and delta < 0 :
if (int(b+t_2*ray[1])/2 == int((b+t_2*ray[1]) / 2) and not int(a+t_2*ray[0]) / 2 == int((a+t_2*ray[0]) / 2)) or (not int(b+t_2*ray[1])/2 == int((b+t_2*ray[1]) / 2) and int(a+t_2*ray[0]) / 2 == int((a+t_2*ray[0]) / 2)) :
color = (0,255,0)
else :
color = (255,0,0)
inter_sph[0] = a+t_2*ray[0]
inter_sph[1] = b+t_2*ray[1]
inter_sph[2] = c+t_2*ray[2]
light_ray[0] = light[0] - inter_sph[0]
light_ray[1] = light[1] - inter_sph[1]
light_ray[2] = light[2] - inter_sph[2]
delta_2 = 4*pow(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2], 2) - 4*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))*(-2*inter_sph[0]*sphere[0] - 2*inter_sph[1]*sphere[1] - 2*inter_sph[2]*sphere[2] + pow(inter_sph[0],2) + pow(inter_sph[1],2) + pow(inter_sph[2],2) + pow(sphere[0],2) + pow(sphere[1],2) + pow(sphere[2],2) - pow(sphere[3],2))
if delta_2 > 0 :
if color == (255, 0, 0) :
color = (100, 0, 0)
else :
color = (0, 100, 0)
elif delta >= 0 and t_2 <= 0 :
inter_sph[0] = a+t*ray[0]
inter_sph[1] = b+t*ray[1]
inter_sph[2] = c+t*ray[2]
light_ray[0] = light[0] - inter_sph[0]
light_ray[1] = light[1] - inter_sph[1]
light_ray[2] = light[2] - inter_sph[2]
if sphere[4] == 0 :
delta_2 = 4*pow(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2], 2) - 4*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))*(-2*inter_sph[0]*sphere[0] - 2*inter_sph[1]*sphere[1] - 2*inter_sph[2]*sphere[2] + pow(inter_sph[0],2) + pow(inter_sph[1],2) + pow(inter_sph[2],2) + pow(sphere[0],2) + pow(sphere[1],2) + pow(sphere[2],2) - pow(sphere[3],2))
if delta_2 >= 0 :
r_1 = (-2*(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2]) - math.sqrt(delta_2)) / 2*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))
r_2 = (-2*(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2]) + math.sqrt(delta_2)) / 2*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))
if abs(r_1) > abs(r_2) :
color = (0,0,255)
else :
color = (0,0,255 - (r_2*255)/(abs(r_1)+r_2))
else :
color = (0,0,255)
else :
diam_vec[0] = inter_sph[0] - sphere[0]
diam_vec[1] = inter_sph[1] - sphere[1]
diam_vec[2] = inter_sph[2] - sphere[2]
k = (diam_vec[0]*(a - sphere[0]) + diam_vec[1]*(b - sphere[1]) + diam_vec[2]*(c - sphere[2])) / (pow(diam_vec[0], 2) + pow(diam_vec[1], 2) + pow(diam_vec[2], 2))
l = (pow(diam_vec[0], 2) + pow(diam_vec[1], 2) + pow(diam_vec[2], 2))*pow(k, 2) + 2*(diam_vec[0]*(a - sphere[0]) + diam_vec[1]*(b - sphere[1]) + diam_vec[2]*(c - sphere[2])) + (pow(sphere[0] - a, 2) + pow(sphere[1] - b, 2) + pow(sphere[2] - c, 2))
proj = [k*diam_vec[0] + sphere[0] , k*diam_vec[1] + sphere[1] , k*diam_vec[2] + sphere[2]]
refl = [2*(proj[0] - a) + a , 2*(proj[1] - b) + b , 2*(proj[2] - c) + c]
reflect = [refl[0] - inter_sph[0] , refl[1] - inter_sph[1] , refl[2] - inter_sph[2]]
if plane[0]*reflect[0] + plane[1]*reflect[1] + plane[2]*reflect[2] != 0 :
t_2 = -(plane[0]*inter_sph[0] + plane[1]*inter_sph[1] + plane[2]*inter_sph[2] + plane[3]) / (plane[0]*reflect[0] + plane[1]*reflect[1] + plane[2]*reflect[2])
if t_2 > 0 :
if (int(inter_sph[1]+t_2*reflect[1])/2 == int((inter_sph[1]+t_2*reflect[1]) / 2) and not int(inter_sph[0]+t_2*reflect[0]) / 2 == int((inter_sph[0]+t_2*reflect[0]) / 2)) or (not int(inter_sph[1]+t_2*reflect[1])/2 == int((inter_sph[1]+t_2*reflect[1]) / 2) and int(inter_sph[0]+t_2*reflect[0]) / 2 == int((inter_sph[0]+t_2*reflect[0]) / 2)):
color = (0,255,0)
else :
color = (255,0,0)
inter_sph[0] = inter_sph[0]+t_2*reflect[0]
inter_sph[1] = inter_sph[1]+t_2*reflect[1]
inter_sph[2] = inter_sph[2]+t_2*reflect[2]
light_ray[0] = light[0] - inter_sph[0]
light_ray[1] = light[1] - inter_sph[1]
light_ray[2] = light[2] - inter_sph[2]
delta_2 = 4*pow(inter_sph[0]*light_ray[0] + inter_sph[1]*light_ray[1] + inter_sph[2]*light_ray[2] - light_ray[0]*sphere[0] - light_ray[1]*sphere[1] - light_ray[2]*sphere[2], 2) - 4*(pow(light_ray[0], 2) + pow(light_ray[1], 2) + pow(light_ray[2], 2))*(-2*inter_sph[0]*sphere[0] - 2*inter_sph[1]*sphere[1] - 2*inter_sph[2]*sphere[2] + pow(inter_sph[0],2) + pow(inter_sph[1],2) + pow(inter_sph[2],2) + pow(sphere[0],2) + pow(sphere[1],2) + pow(sphere[2],2) - pow(sphere[3],2))
if delta_2 >= 0 :
if color == (255, 0, 0) :
color = (100, 0, 0)
else :
color = (0, 100, 0)
else :
color = (0, 0, 0)
else :
color = (0,0,0)
plt.set_pixel(x, y, color)
plt.show_screen()
Citer : Posté le 10/04/2020 09:27 | #
Ok, merci.
Tu prévois de nous le rajouter à tes autres programmes sur le site ?
Citer : Posté le 10/04/2020 09:52 | #
Wow, pété !!
Et la question qui tue : ça prend combien de temps ?
Citer : Posté le 10/04/2020 09:56 | #
@Lephenixnoir : heu ben c'est à dire... 2 à 3 minutes ?
Citer : Posté le 10/04/2020 10:02 | #
Pas mal du tout alors comme performances.
Wow, pété !!
Et la question qui tue : ça prend combien de temps ?
Justement, ça me fait penser qu'il faudrait que Casio nous rajoute le module time pour des mesures plus précises, présent sur toute la concurrence.
Citer : Posté le 10/04/2020 10:03 | #
Je pense que notre petit concours de démos va être animé. C'est toute une branche qui s'ouvre ici (au détail près qu'on n'a pas de getkey() ^^" ) !
Citer : Posté le 10/04/2020 10:05 | #
Ouais pas de GetKey et de Time c tendu pour faire plus complexe..
-Planétarium 2
Citer : Posté le 10/04/2020 10:08 | #
Pour le rendu plein écran 396x224 pixels, j'ai 6mins45 à la montre (Casio) par ici, sans aucun overclocking :
Ajouté le 10/04/2020 à 10:42 :
Au passage, j'ai fais quelques tests, et si on se base sur get_pixel(x, y) qui retourne None lorsque le pixel est hors de la zone de dessin, on tombe sur une zone utilisable de 384×192 pixels sur la G90+E
Ça vaut peut être le coup de l'ajouter dans l'article
...
Mais pour un script destiné à tourner sur différents modèles pour un concours de rentrée ou autre, il faut savoir que cette astuce formidable ne marche apparemment pas sur NumWorks.
Voici une première tentative d'un code compatible qui détecte la taille de la zone affichable, et pourrait donc être utilisé par tous les scripts se voulant multi-plateformes :
import ti_graphics as scr
getPixel = scr.getPixel
setPixel = scr.setPixel
except ImportError:
try:
import casioplot as scr
except ImportError:
import kandinsky as scr
getPixel = scr.get_pixel
setPixel = scr.set_pixel
def isPixelOK(c):
return c is not None and c != (0, 0, 0)
def getscreen():
x, y, dx, dy = 0, 0, 1, 1
while(dx or dy):
setPixel(x - (dx==0), y - (dy==0), (255, 255, 255))
c = getPixel(x - (dx==0), y - (dy==0))
if not isPixelOK(c):
if isPixelOK(getPixel(x,y - 1)): dy = 0
else: dx = 0
x += dx
y += dy
return (x, y)
Première pierre du concours de rentrée 2020.
Citer : Posté le 10/04/2020 10:44 | #
Il y à une lib graphique en python sur ti ? (officielle ?)
-Planétarium 2