Résultat du concours de rentrée 2019 - Épreuve de tracé !
Posté le 09/11/2019 11:19
Salut à la communauté ! Il est l'heure de passer en revue les participations, méthodes et classement de la première épreuve de notre concours de rentrée annuel. 
Le sujet de
l'épreuve de tracé était de reproduire avec le code le plus court possible l'image suivante sur fx-92 Scientifique Collège+.
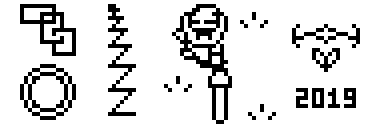
Comme l'année dernière, nous avons reçu pas moins de
93 participations de 18 personnes, présentant de nombreuses techniques pour court-circuiter le dessin et tracer toujours avec toujours moins.
La majorité d'entre vous a travaillé sur la fx-92 SC+ ou son émulateur (15), avec quelques participations en Scratch (1) et Python (2) qui ont été traduites semi-automatiquement vers le langage de la fx-92 SC+.
Alors voyons dès maintenant le classement et les méthodes que vous avez utilisées pour parvenir à vos fins ! Nous avons rédigé un commentaire succinct sur chaque programme avec l'animation du tracé qu'il réalise. Plusieurs d'entre vous ont déjà décrit leurs méthodes en détail. N'hésitez pas à ajouter vos techniques dans les commentaires !
 (Pour le choix des lots, voyez à la fin de l'article !)
Le classement
17.
(Pour le choix des lots, voyez à la fin de l'article !)
Le classement
17. On commence tranquillement avec la
participation de
CaptainLuigi. La façon la plus naturelle d'attaquer une série de rectangles est de tourner de 90° entre chaque trait. On verra vite que ça se chaîne assez bien malgré les irrégularités. Ici l'oubli dommage c'est le curseur, qui dessine beaucoup de pixels superflus. Quatre personnes en tout ont omis de le masquer en le déplaçant hors de l'écran...


 16.
16. Avec
Leno (
TI-Planet,
Planète Casio) sur fx-92+ Spéciale Collège, on commence à trouver les techniques permettant de tracer rapidement les cercles en profitant du fait que la position du crayon et l'angle d'orientation de la tortue sont bien plus précis que 1 pixel ou 1 degré. On peut donc tourner de 18.43 degrés ou avancer de 3.2 pixels à son avantage pour tracer tout le cercle à l'aide d'une boucle régulière. La même technique est utilisée pour la série de Z, qui n'est malheureusement pas au bon endroit par rapport au cercle.
326 points.

 15.
15. On fait maintenant un bond dans le score, jusqu'à
1344 points points avec
Ptitjoz (
TI-Planet,
Planète Casio). Ici on a les rectangles complets, les cercles, les Z et le texte. Ici on se permet de reproduire une image approximative pour gratter des points : c'était le but de l'épreuve. Dans cette participation, pas de rotation ou pas avec des valeurs décimales, le cercle intérieur rate donc quelques pixels. Pour les rectangles, c'était l'effet attendu : on pensait que les deux pixels en trop valaient les instructions économisées. Voyons ce que vous en avez pensé...



Ptitjoz a écrit :Je vous explique comment je voulais procéder... Voila la méthode mais faute de temps
(je n'en expliquerai pas les raisons...  )
) je n'ai fait que quelques tests que j'aurais essayé d'optimiser. Une de mes participations où l'on peut voir un peu de ce code est :
ici. Le principe retenu est que chaque pixel dessiné vaut
1 et chaque pixel non dessiné vaut
0. Mon idée était d'encoder l'image colonne par colonne en transformant le binaire obtenu en décimal et de le stocker dans une variable. Ensuite avec une boucle pour chaque colonne je décodais la variable en binaire point par point et j'affichai le pixel si la valeur était
1 sinon ne je l'affichais pas. Le code parlera mieux que mes explications.
Voilà, point final pour cette année. Merci à tous.
(message original)
14. Juste au-dessus de ce score,
Zocipal attaque justement les rectangles au pixel près. La technique est la même, sauf que les rectangles font maintenant 5 côtés pour ainsi dire. Les cercles sont cependant plus manuels, avec essentiellement des angles droits et des levées et posées fréquentes de stylo. Ça prend de la place mais les points le valent bien, puisque chaque pixel rapporte 10 points contre 1 seul point perdu par octet.
1367 points. 

 13.
13. Toujours au coude-à-coude,
Edgar13 prend la place suivante. On voit ici les premières attaques sérieuses sur le sprite de Link, pour l'instant en exploitant les lignes continues les plus longues dans l'image. C'est un bon moyen d'accumuler les pixels à moindre coût, sans tenter de reproduire toute l'image. On a la même stratégie pour réduire le texte en utilisant des formes simples à programmer, appliquée finement. Bien joué !
1418 points. 

Edgar13 a écrit :Pour les rectangles j'ai fait très simple juste des petites boucles de 2:
2→M
10→F
Aller à x=M; y=F
Stylo écrit
S'orienter à 270 degrés
Répéter 2
Avancer de 4 pixels
Tourner de ↺ -90 degrés
Avancer de 8 pixels
Tourner de ↺ -90 degrés
⤴
Stylo relevé
Aller à x=4; y=8
Stylo écrit
Répéter 2
Avancer de 7 pixels
Tourner de ↺ -90 degrés
Avancer de 5 pixels
Tourner de ↺ -90 degrés
⤴
Stylo relevé
Aller à x=7; y=4
Stylo écrit
Répéter 2
Avancer de 6 pixels
Tourner de ↺ -90 degrés
Avancer de 5 pixels
Tourner de ↺ -90 degrés
⤴
Stylo relevé
Pour les Z par contre j'ai pas mal réfléchi et je les ai tracé avec X et Y, ce qui m'a donné un code assez court:
16→M
Aller à x=M; y=F
Stylo écrit
2→A
Répéter 6
F-(A-1)→F
Aller à x=M; y=F
S'orienter à 0 degrés
Avancer de A pixels
Si A<7 Alors
A+1→A
Fin
⤴
Ensuite j'ai surtout essayé de faire des rectangle avec des boucles :
Avancer de -1 pixels
Aller à x=16; y=-17
Avancer de 6 pixels
Stylo relevé
Aller à x=42; y=-19
Stylo écrit
Répéter 2
Avancer de 3 pixels
Tourner de ↺ 90 degrés
Avancer de 9 pixels
Tourner de ↺ 90 degrés
⤴
Stylo relevé
Aller à x=40; y=-5
Stylo écrit
Aller à x=32; y=3
Stylo relevé
Aller à x=67; y=-15
Stylo écrit
Répéter 2
Avancer de 2 pixels
Tourner de ↺ 90 degrés
Avancer de 4 pixels
Tourner de ↺ 90 degrés
⤴
Stylo relevé
Aller à x=41; y=-5
Stylo écrit
Répéter 4
Avancer de 3 pixels
Tourner de ↺ 90 degrés
⤴
Stylo relevé
Aller à x=63; y=-13
Stylo écrit
Répéter 3
Avancer de 2 pixels
Tourner de ↺ 90 degrés
⤴
Stylo relevé
Ensuite j'ai dessiné le 2019 de façon basique et simple juste en avançant et en relevant le stylo pour passer à une autre lettre :
Aller à x=63; y=-13
Stylo écrit
Répéter 2
Avancer de 2 pixels
Tourner de ↺ 90 degrés
⤴
Stylo relevé
Aller à x=71; y=-15
Stylo écrit
S'orienter à 0 degrés
Avancer de 2 pixels
Avancer de -1 pixels
Tourner de ↺ 90 degrés
Avancer de 4 pixels
Stylo relevé
Aller à x=75; y=-15
S'orienter à 0 degrés
Stylo écrit
Avancer de 2 pixels
Tourner de ↺ 90 degrés
Avancer de 4 pixels
Tourner de ↺ 90 degrés
Répéter 3
Avancer de 2 pixels
Tourner de ↺ 90 degrés
⤴
Stylo relevé
Aller à x=38; y=3
Stylo écrit
S'orienter à 0 degrés
Répéter 2
Avancer de 3 pixels
Tourner de ↺ 90 degrés
Avancer de 1 pixels
Tourner de ↺ 90 degrés
⤴
Stylo relevé
Aller à x=35; y=0
Stylo écrit
Avancer de 9 pixels
Tourner de ↺ -90 degrés
Avancer de 6 pixels
Et pour finir j'ai fait sortir la flèche:

Stylo relevé
Avancer de 99 pixels
Mais j'ai eu un problème de temps et j'aurais pu faire mieux il me restait 200 octets.
12. LePetitMage nous propose la première
participation en Scratch (lien direct
t13.sb3). Une fois
retranscrite sur fx-92+ Spéciale Collège, on retrouve plusieurs éléments précédents : sacrifier des pixels inutiles sur les rectangles, tailler dans le vif sur le sprite de Link, et on a même la chance d'apercevoir un brin d'herbe
(tiré des premières générations de Pokémon !) au-dessus du 2019. Les techniques pour tracer les cercles avec des avancées décimales sont plus subtiles à reproduire sur Sractch, qui a des règles de rendu un peu différentes... et également un plus grand écran. On s'en sort quand même avec un score très honorable, malgré la traduction, l'écran tronqué et le curseur en plus. Bel effort ! 1610 points.


LePetitMage a écrit :Bonjour,
je suis le dernier parmi ceux qui ont un lot et je vous présente ici ma méthode.
Merci à Lephe pour l'animation trouvable ici :
https://i.imgur.com/Tx4ABSR.gif
J'ai commencé par les rectangles qui s'emboîtent en définissant un pixel qui sera l'origine d'un repère.
Stylo écrit
Aller à x=0; y=-7
Avancer de 5 pixels
Avancer de -2 pixels
Aller à x=3; y=-10
Avancer de 5 pixels
Aller à x=8; y=-4
Avancer de -5 pixels
Avancer de 2 pixels
Aller à x=5; y=0
Avancer de -5 pixels
Aller à x=0; y=-2
Avancer de 3 pixels
Aller à x=3; y=2
Avancer de -8 pixels
Aller à x=-5; y=-2
Avancer de 4 pixels
Vous avez sûrement remarqué que :
-je n'ai pas utilisé de "Tourner de ..." pour économiser des lignes. Pour se déplacer vers la droite ou vers la gauche, j'avance d'un nombre positif ou négatif de pixels. Pour monter ou descendre, j'écris les coordonnées en fonction de l'origine du repère. C'est une technique que je vais utiliser un peu partout.
-j'avance parfois d'un nombre de pixel puis je recule tout de suite après. C'est pour gratter les pixels des "cornes" entre les rectangles.
J'ai continué avec les Z, où il n'y a pas spécialement de remarque à faire.
Avancer de 1 pixels
Aller à x=17; y=2
Stylo écrit
1→A
√(2→B
Avancer de 1 pixels
Répéter 5
A+1→A
S'orienter à 225 degrés
Avancer de B×(A-1) pixels
S'orienter à 0 degrés
Avancer de A pixels
⤴
Aller à x=17; y=-19
Avancer de 6 pixels
Aller à x=17; y=-25
Avancer de 5 pixels
Et pour les deux cercles, je ne me suis pas embêté avec les angles et j'ai laissé de côté 4 pixels.
Aller à x=0; y=-26
Répéter 4
Stylo écrit
Avancer de 3 pixels
Tourner de ↺ 45 degrés
Avancer de B pixels
Tourner de ↺ -45 degrés
Avancer de 1 pixels
Tourner de ↺ 45 degrés
Avancer de B×2 pixels
Tourner de ↺ 45 degrés
Avancer de1pixels
Tourner de ↺ -45 degrés
Avancer de B-B÷Abs(B pixels
Stylo relevé
Avancer de B÷Abs(B pixels
Tourner de ↺ 45 degrés
⤴
Aller à x=0; y=-24
Répéter 4
Stylo écrit
Avancer de 3 pixels
Tourner de ↺ 45 degrés
Avancer de B×3-B÷Abs(B pixels
Stylo relevé
Avancer de B÷Abs(B pixels
Tourner de ↺ 45 degrés
⤴
J'ai continué avec le link en ne dessinant que les diagonales les plus généreuses en points (vous le remarquerez facilement dans l'animation de Lephe).
Aller à x=43; y=-26
Stylo écrit
Aller à x=43; y=-13
Avancer de 2 pixels
Avancer de -4 pixels
Aller à x=33; y=-5
Aller à x=40; y=2
Avancer de 4 pixels
Aller à x=44; y=-4
Avancer de -7 pixels
Aller à x=37; y=-2
Avancer de 5 pixels
Stylo relevé
Avancer de 1 pixels
Aller à x=46; y=-26
Stylo écrit
Aller à x=46; y=-12
J'ai ensuite dessiné 2019 en sacrifiant quelques pixels (certains non dessiné et d'autres en plus pour éviter les "Stylo levé" et "Stylo écrit").
Aller à x=64; y=-19
Stylo écrit
Avancer de 2 pixels
Aller à x=66; y=-21
Avancer de -2 pixels
Aller à x=64; y=-23
Avancer de 6 pixels
Aller à x=70; y=-19
Avancer de -2 pixels
Aller à x=68; y=-23
Avancer de 5 pixels
Aller à x=73; y=-19
Aller à x=73; y=-23
Avancer de 5 pixels
Aller à x=78; y=-19
Avancer de -2 pixels
Aller à x=76; y=-21
Avancer de 1 pixels
Et pour finir, le coeur avec la même technique que les rectangles mais aussi en se déplaçant sans tourner.
Aller à x=71; y=-14
Stylo écrit
Aller à x=71; y=-11
Aller à x=73; y=-9
Avancer de 1 pixels
Aller à x=74; y=-11
Aller à x=71; y=-14
Aller à x=68; y=-11
Aller à x=68; y=-9
Avancer de 1 pixels
Aller à x=71; y=-11
J'ai participé sur Scratch, l'avantage est que je suis plus à l'aise sur Scratch et que c'est plus amusant de glisser des blocs.
Par contre, je ne savais pas que plusieurs bouts de mon dessin seraient en dehors de l'écran et que ces pixels ne sont pas compté, et que la conversion depuis Scratch implique de rajouter des lignes.
(message original)
11. Et on embraye directement sur la première participation Python par
Afyu. Le
code original (lien direct
t14.py) trace l'image complète, mais fait 2094 octets une fois
traduit. Il faut donc arrêter le script à un peu plus de la moitié. La plupart du tracé utilise des instructions simples et n'hésite pas à utiliser
«Aller à» comme source primaire de déplacement, plutôt que
«Avancer de». Si les changements de direction sont trop fréquents, c'est en effet bien plus court
(5 octets plus la taille des coordonnées contre 6 octets plus la taille de l'angle et celle du pas), ce qui n'était pas évident en première approche. 1635 points.



Afyu a écrit :Mon script n'est clairement pas optimisé, et j'en suis conscient. D'abord, j'ai découvert le défi seulement quelques jours avant la fin du concours. J'ai voulu effectuer quelques tests sur une fx92+ sc mais je n'en ai pas, je ne connais personne qui en a une et je n'ai pas pu essayer sur émulateur parce que mon Linux n'est pas à jour et je ne peux pas installer Wine. Ce n'est pas une excuse mais ça explique certains (nombreux) points plutôt impertinents et peu optimisés. J'ai donc écrit mon script en Python avec le module Turtle, en utilisant le support prévu pour la NumWorks proposé pour le concours.
Je cache la tortue (et j'aurais bien aimé qu'une fonction existe pour cacher la flèche sur la fx92+, dommage). Je commence avec le zigzag (éclair ?). La commande fd() correspond à "Avancer de".
goto(27,7)
pendown()
i=1
fd(1)
Pour tracer le zigzag, les déplacements horizontaux sont faits avec fd(), et les déplacements en biais sont faits avec goto(x,y). Ça économise des changements de direction (et encore une fois, sans pouvoir vérifier sur une vraie fx92+, je ne me suis pas risqué à choisir un angle ou un pas qui risquaient de ne pas convenir ou d'être interprété différemment par une fx92+).
On souhaite descendre de 1, puis de 2, puis de 3, puis de 4... Donc le décalage par rapport au début du zigzag en haut est de 1, puis de 1+2, puis de 1+2+3, puis de 1+2+3+4...
Le décalage total vertical est donc la somme des premiers entiers naturels, qui peut s'écrire sous la forme : 1+2+3+...+n=n(n+1)/2, d'où le i*(i+1)/2.
J'ai envisagé de remplacer cette fraction par un simple goto(28,y-i) mais je ne savais pas comment écrire ça, sachant que dans mon script en Python il n'y a pas de y et je ne suis pas sûr que Turtle comprenne ce genre d'instruction avec y. Ah, si seulement j'avais eu une fx92+ sous la main ! Le dernier virage est en dehors de la boucle pour éviter d'avancer de 7.
while i<7:
fd(i)
goto(28,7-i*(i+1)/2) #goto(28,y-i)
i=i+1
fd(6)
goto(28,-20)
fd(6)
penup()
De même, pour les polygônes, les déplacements horizontaux sont faits avec fd() et les déplacements verticaux sont faits avec goto(x,y).
goto(14,-1)
pendown()
goto(14,1)
fd(5)
goto(19,-5)
fd(-5)
goto(14,-2)
penup()
goto(16,0)
pendown()
goto(16,-2)
fd(-5)
goto(11,5)
fd(3)
goto(14,7)
fd(-8)
goto(6,3)
fd(8)
goto(14,5)
fd(2)
goto(16,1)
penup()
Pour le 2019, j'ai tracé segment par segment, avec une boucle pour tracer le "0" en deux fois et une autre pour tracer le haut du "9" en 4 fois.
goto(74,-14)
pendown()
fd(3)
goto(77,-16)
fd(-2)
goto(75,-18)
fd(2)
penup()
fd(2)
pendown()
for k in range(2): #répéter 2
fd(2)
lt(90)
fd(4)
lt(90) #la tortue regarde de nouveau vers la droite (orientation à 0°)
penup()
fd(3)
pendown()
fd(3)
fd(-1)
lt(90)
fd(4)
goto(83,-15)
penup()
goto(86,-18)
pendown()
lt(-90)
fd(3)
lt(90)
fd(2)
for l in range(4): #répéter 4
fd(2)
lt(90)
penup()
Pour la fée, j'ai enchaîné des segments. Je me pose en bas, je trace le segment vertical, puis je pars à droite, je redescends en biais, je repars à gauche en biais et je termine en revenant vers le milieu. Les déplacements verticaux sont faits avec fd() et je profite du fait que la tortue regarde vers le haut (orientation 90°) à la fin du tracé du "2019".
goto(82,-10)
pendown()
fd(4)
goto(84,-4)
goto(85,-4)
fd(-2)
goto(82,-9)
goto(79,-6)
fd(2)
goto(80,-4)
goto(82,-6)
penup()
Pour les cercles, j'ai utilisé des boucles et de trop nombreux déplacements de 1. Faute de pouvoir tester sur une vraie fx92+ ou sur émulateur, j'ai préféré m'assurer que le tracé était correct et je n'ai pas pu trouver (ni même chercher) le pas et l'angle qui auraient permis de tout tracer avec une seule boucle.
J'ai tout de même utilisé l'astuce que le grand cercle ressemble au petit mais comme si on l'avait découpé en 4, si on avait éloigné les 4 morceaux et si on avait ajouté quelque chose entre deux morceaux adjacents. D'où la partie "Si q>4" et la partie "Si q=5" qui permet de se décaler pour se mettre sur le tracé du grand cercle.
goto(8,-12)
setheading(0) # on oriente la tortue à 0° (elle regarde vers la droite)
q=1
while q<9: # répéter 9
if q==5:
goto(6,-12)
pendown()
fd(1)
lt(90)
fd(1)
lt(-90)
if q>4:
penup()
fd(1)
lt(90)
pendown()
fd(1)
penup()
fd(1)
lt(-90)
pendown()
fd(1)
fd(1)
penup()
lt(90)
fd(1)
lt(-90)
pendown()
fd(4)
penup()
fd(1)
lt(-90)
q=q+1
Pour Link, j'ai essayé de le tracer segment par segment (comme une ligne brisée) en relevant le stylo un minimum de fois. Les changements d'orientation très nombreux sont remplacés par des goto(x,y). Et dans l'histoire, j'ai oublié 2 pixels vers le haut à gauche.
setheading(90) #on oriente la tortue à 90° (donc elle regarde vers le haut)
goto(54,-4)
pendown()
goto(57,-7)
goto(53,-11)
fd(-2)
goto(57,-13)
fd(-8)
goto(56,-22)
goto(55,-22)
goto(54,-21)
fd(8)
goto(58,-13)
fd(2)
goto(57,-10)
fd(1)
goto(54,-9)
goto(56,-7)
fd(4)
goto(55,-2)
goto(56,-1)
fd(1)
goto(57,1)
fd(3)
goto(54,7)
goto(50,7)
goto(48,5)
goto(47,5)
goto(46,4)
fd(-3)
goto(45,1)
goto(44,0)
goto(52,-8)
goto(54,-8)
goto(51,-8)
goto(49,-6)
goto(47,-6)
goto(46,-5)
fd(1)
goto(47,-4)
fd(3)
goto(49,-3)
goto(54,-3)
goto(53,-4)
fd(-4)
goto(52,-7)
goto(54,-5)
penup()
goto(48,5)
pendown()
fd(-2)
lt(-90)
fd(2)
penup()
fd(1)
pendown()
fd(4)
lt(90)
fd(2)
lt(90)
fd(1)
penup()
goto(56,3)
pendown()
goto(53,0)
fd(3)
goto(48,2)
penup()
goto(50,-2)
pendown()
goto(50,1)
fd(-3)
goto(53,-1)
penup()
goto(45,2)
pendown()
goto(47,0)
penup()
goto(48,4)
pendown()
goto(50,6)
penup()
Pour le vaisseau (ou logo, ou je sais pas trop quoi

), j'ai utilisé la symétrie centrale de la zone centrale mais en traçant la figure ligne par ligne (comme des lignes horitontales de pointillés) puis j'ai tracé les deux parenthèses et enfin les deux traits obliques manquants.
goto(74,2)
setheading(0)
q=0
while q<2:
pendown()
fd(1)
penup()
fd(6)
if q==0:
pendown()
fd(1)
penup()
fd(6)
pendown()
fd(1)
penup()
goto(90,-3)
lt(180)
q=q+1
goto(79,1)
for r in range(2):
for s in range(2):
pendown()
fd(2)
penup()
fd(1)
goto(85,-1)
lt(180)
goto(76,0)
for t in range(2):
pendown()
fd(3)
penup()
fd(5)
goto(74,-1)
for u in range(2):
pendown()
fd(2)
penup()
fd(11)
goto(74,-3)
for v in range(2):
pendown()
setheading(90)
fd(4)
penup()
goto(90,-3)
goto(82,-3)
pendown()
fd(1)
penup()
Pour les herbes, je parcours 3 fois une boucle qui met à jour les coordonnées du point de départ à chaque fois.
a=42
b=-15
w=0
while w<3:
goto(a+2,b)
pendown()
goto(a,b+2)
penup()
goto(a+4,b)
pendown()
goto(a+6,b+2)
penup()
goto(a+3,b+2)
pendown()
fd(2)
penup()
if w==0:
a=61
b=1
if w==1:
a=63
b=-22
w=w+1
10. Juste au-dessus, on rentre dans le top 10, avec
Amiga68000 sur la fx-92+ Spéciale Collège. Et là, surprise ! Un
programme composé en moitié d'une longue suite de
«Aller à» explicites remporte pas moins de 1722 points. Quelques angles décimaux sont utilisés pour les cercles, mais c'est tout. Ce programme simple en apparence fait facilement tomber la moitié du sprite de Link. Difficile de savoir si la séquence de lignes a été générée automatiquement ou cherchée à la main. En tous cas c'est une piste que l'on attendait fermement et qui a servi à choisir le barème de l'épreuve.
Eh oui, même à 1 contre 10, le code compliqué coûte vite cher ! 


Amiga68000 a écrit :Je vous partage mon code pour faire les carrés et les cercles. Pour les carrés j'ai pas eu le temps de regarder l'utilisation des boucles. Pour les cercles, j'ai utilisé des boucles imbriquées. Les 4 pixels dans les coins du cercle ne sont pas tracés, je suis preneur d'un code plus optimum. Le gros pâté c'est le pointeur flèche !
script
Voici le code pour les ZZZ :
script. J'ai utilisé les boucles avec des coordonnées
(x,y) le mieux aurait été d'utiliser les
(orientation, déplacement). Là encore je suis preneur d'optimisation.
Chapeau à celui qui a presque tout tracé.

(message original)
9. À la 9ème place,
Éléonore D. score
1958 points en combinant la simplicité des
«Aller à» avec trois boucles intelligentes. La première permet de tracer la décoration au-dessus du 2019, et la touffe d'herbe d'un coup en profitant de la symétrie. Les deux autres sont des formes super compactes pour le tracé des cercles : 36 pas de 1.12 pixel séparés de 9.9 degrés chacun, et 28 pas de 1 pixel séparés de 12.75 degrés chacun. Cela laisse amplement la place de s'attaquer à Link.



Éléonore D. a écrit :
Pour ma part,je rien fais d'extraordinaire, j'ai beaucoup utilisé de ''aller à''.
8. Une bonne centaine plus haut à 2070 points,
Clément C. propose un
programme quasi-identique qui se distingue en choisissant mieux les parties de Link et en profitant de l'espace libéré pour tracer plus en détail la décoration symétrique sur la droite.


Clément C. a écrit :
J'ai essayé de faire de mon mieux(donc rien de bien compliquer) pour les cercles j'ai fais comme Amiga68000.
7. On fait ensuite un nouveau bond pour atteindre la 7ème place où le premier participant à cette épreuve,
Encephalogramme, atteint les
2227 points. Ici moins de souci de finesse, on factorise le dessin dans des boucles et on couvre les pixels le plus vite possible. On remarque une boucle bien compacte pour le tracé de plusieurs rectangles à la suite. Les octets économisés compensent les pixels sacrifiés. Comme quoi on peut aller loin avec des outils simples : bravo !



Encephalogramme a écrit :Je pense que ma méthode est assez basique, et mon but était donc d'optimiser avec des boucles et en choisissant les meilleurs morceaux du dessin.
Je mets ici les parties du code de façon séparées pour mieux visualiser
Cette portion du code permet de tracer le petit et le grand cercle, avec des valeurs étranges, comme "avancer de 4.5 pixels", mais ça marche :
Répéter 4
Avancer de 3 pixels
Tourner de ↺ -34 degrés
Avancer de 4,5 pixels
Tourner de ↺ -31 degrés
Avancer de 3 pixels
Tourner de ↺ -26 degrés
⤴
S'orienter à 0 degrés
Stylo relevé
Aller à x=x; y=y-2
Stylo écrit
Répéter 4
Avancer de 1 pixels
Tourner de ↺ -14 degrés
Avancer de 4 pixels
Tourner de ↺ -60 degrés
Avancer de 2,5 pixels
Tourner de ↺ -16 degrés
⤴
Ici, ça permet de tracer les Z avec des boucles, encore une fois pour gagner de la place :
1→A
Répéter 5
Aller à x=x+A; y=y
Aller à x=x-A; y=y-A
A+1→A
⤴
Répéter 2
Aller à x=x+A; y=y
Aller à x=x-A; y=y-A
⤴
Aller à x=x+A; y=y
Stylo relevé
Aller à x=x-28; y=y+27
Le code qui suit permet de tracer les 3 rectangles au-dessus des cercles, le but est de faire ça en peu de place, même si il faut pour cela tracer des pixels qui devaient rester blancs :
Répéter 2
Avancer de 8 pixels
Tourner de ↺ -90 degrés
Avancer de 4 pixels
Tourner de ↺ -90 degrés
⤴
Stylo relevé
Aller à x=x+5; y=y-9
Stylo écrit
7→A
Répéter 2
Répéter 2
Avancer de 5 pixels
Tourner de ↺ 90 degrés
Avancer de A pixels
Tourner de ↺ 90 degrés
⤴
A-1→A
Stylo relevé
Aller à x=x+3; y=y-3
Stylo écrit
⤴
Le plus "interessant" est passé, à partir de là c'est le tracé d'une partie du link et de 2019, en utilisant principalement des "aller à", ce qui permet d'aller aussi bien en haut, qu'en bas, mais aussi a droite, à gauche ainsi qu'en diaguonale. L'avantage, c'est que je n'ai pas besoin de changer d'angle pour tracer les figures, et gagne donc facilement des octets.
J'aurais pu avoir plus de points en mettant des "aller à" avec des coordonnées précises et pas relatives à la position actuelle, car d'après les participations des autres cela consomme moins d'octets, mais je m'en suis pas trop mal sorti :3
6. À la 6ème place, une
participation très dense de
Astrostellar obtient 2405 points. Plein d'astuces sont utilisées ici, mais la plus unique est certainement l'exploitation de la symétrie dans la tête et l'épée de Link, sur une seule boucle ! Avec deux variables de contrôle le même code trace une large moitié du sprite en un temps record. On reconnaît en fait une astuce générale consistant à exécuter une boucle deux fois en changeant le paramètre entre les deux tours. Le niveau de régularité requis est très faible
(contrairement à des boucles ayant au moins 3 tours) et ça factorise efficacement le code. Cette participation est aussi la seule, il nous semble, à utiliser des
«Avancer de» pour tracer les Z.


Astrostellar a écrit :J'ai tout d'abord essayer de tracer dans des programmes indépendants les différentes parties de l'image, à savoir les rectangles, les ronds, les Z, Link, 2019 et le petit patern symétrique avec le coeur en dessous. Malheureusement, une fois tous les bouts de programme réunis en un seul, celui-ci dépassait largement la limite des 900 octets. J'ai donc dû faire des sacrifices pour gagner des octets en perdant un minimum de points.
J'ai effectivement utilisé une boucle pour tracer le Link. En effet, j'avais remarqué la symétrie de son visage. Je fais ainsi simplement une boucle qui trace la moitié du Link avant de changer ma valeur A (qui vaut 1 au début) en -1 pour pouvoir tracer la symétrie (au lieu d'avancer de 3 pixels par exemple, j'avance ainsi de -3 pixels. Je fais ainsi l'exacte inverse

). La variable B vaut 0 lors du premier tour de boucle, puis 1 au second. Celle-ci permet de bien placer ma symétrie : en effet, l'axe de symétrie du visage se situe ENTRE 2 pixels. Si je n'utilisais pas B, la symétrie se tracerait 1 pixel plus loin, autour d'un axe de symétrie qui se situerai alors SUR une verticale de pixels. B me permet ainsi de déplacer de 1 pixel toute ma symétrie. Enfin, C est simplement une valeur qui revient souvent (2A+B) et cela me permet de gagner des octets en initialisant une fois C et la réutiliser au lieu de taper à chaque fois 2A+B. Pour finir, j'ai pivoté au tout début de mon programme de 270 degrés (c'est à dire en vertical vers le bas) pour économiser des Aller à et les remplacer simplement par des Avancer de lorsque j'avais besoin d'aller vers le bas.
Pour les rectangles, j'ai tracé 2 rectangles en une boucle Répéter car ils avaient la même largeur, puis dans une seconde boucle le dernier rectangle. J'ai sacrifié au passage 2 pixels pour ne pas perdre d'octets ;).
J'ai ensuite tracé les ronds. Je fais pivoter mon stylo avant de le faire avancer. Mais les angles de rotation obtenus par calculs, une fois mis dans le programme, ne trace pas un cercle parfait... J'ai alors utilisé un "bidouillage" pour obtenir les angles de rotation... J'ai modifié quelques valeurs d'angles (à 1 ou 2 degrés près) pour que le cercle tracé soit régulier, en essayant plusieurs solutions, d'où les 25, 22, 23 puis 20 degrés de rotation un peu bizarre obtenus grâce à plusieurs essais... Je trace ainsi un quart de cercle, que je mets dans une boucle Répéter 4 fois pour le tracer entièrement. Je passe ensuite au second cercle (celui interne) sans lever mon stylo (économie de 2 lignes Relever puis Abaisser le stylo en sacrifiant un seul pixel).
Pour les Z, j'ai remarqué que la longueur supérieure des Z augmentaient de 1 pixel à chaque niveau en descendant. J'ai donc fait une boucle Répéter 8 fois (pour les 8 Z) avec une incrémentation de 1 à A (la longueur du haut des Z) à chaque tour tant que A n'est pas supérieur à 6 (rang à partir duquel les Z ne s'agrandissent plus). Je pivote à 225 degrés vers la gauche pour me mettre en position pour tracer la diagonale du Z. Sachant que la diagonale a la même longueur que la longueur supérieure de Z, j'avance de √2A (√2 comme pour la diagonale d'un carré), puis je pivote de nouveau pour me retrouver à l'horizontale et tracer le haut de mon Z. Le B est une petite variable qui permet de bien tracer le premier Z.
Pour le 2019, je trace simplement des rectangles à la place des chiffres, sauf pour le 1 (je sacrifie pas mal de pixels, mais je n'avais plus la place de mettre un bon 2019 dans le programme).
Enfin, la dernière boucle permet de répéter le tracé des 2 diagonales de la décoration à droite (ce sont celles qui me permettent de tracer un maximum de pixels en aussi peu de lignes

)
5. On entre dans le top 5 avec
Cala Mar, qui fournit un
programme de 2559 points avec... eh bien pas grand-chose ! Uniquement des
«Aller à», des
«Avancer de», et la technique de tracé de cercles d'
Éléonore . Il trace 6 éléments disjoints en ne relevant le stylo que 7 fois en tout. On s'attendait à cette méthode, mais pas à ce qu'elle soit si efficace ! Et pourtant elle montre qu'il n'y a pas besoin de connaissances de gourou pour tutoyer les meilleurs participants. Félicitations



Cala Mar a écrit :Ah moi j'ai pas fais la même chose qu'
Amiga68000 pour les cercles, j'ai fait:
Aller à x=-30 ; y=-12
Stylo écrit
Répéter 36 fois
Avancer de 1.12 pxl
Tourner de 9.9
⤴
Stylo relevé
S'orienter à 0
Aller à x=-30; y=-10
Stylo écrit
Répéter 28 fois
Avancer de 1 pxl
Tourner de 12.75
⤴
(message original)
4. À partir de la
participation de
Extra44 qui atteint 2673 points, on ne plaisante plus sur les calculs. On commence à utiliser les fonctions de la calculatrice pour diverses optimisations, comme tracer les cercles en calculant tout simplement les sinus et cosinus pour différents angles et rayons. Tout est optimisé aux petits oignons, du choix des lignes jusqu'aux petites régularités permettant d'économiser des octets avec des boucles. Et on termine par une longue suite de
«Aller à» qui trace l'essentiel de Link et de la décoration. Il n'y a quasiment plus un octet à sauver là-dedans.



Extra44 a écrit :Bon pour moi : J'avais fait ma 1ère version sur python/ordi, et comme j'étais à
l'aise (ben oui j'avais de la place... ça me paraissait optimal... c'était beau quoi...), j'avais réussi
(yess  )
) à dessiner correctement le bitmap.
Mais comme quasiment tout le monde ici, le problème est le manque de place. Et quand j'ai vu qu'une instruction moyenne sur la fx-92+ Spéciale Collège faisait au bas mot 10 octets facile
(avec les fins de ligne SVP !); je me suis dit
Arghh !

J'ai eu un autre soucis :
turtle sur python/ordi et turtle sur fx-92+ Spéciale Collège ont un comportement différent sur la dernière position/pixel avant levé du stylo; sur l'ordi : il n'est pas dessiné, sur fx-92+ Spéciale Collège : il l'est.

Du coup une fois passé sur émulateur, je ne suis plus revenu sur le python/ordi !
J'avais attaqué dans cette version les figures par
ordre : en 1er la figure à gauche : les cercles. Après quelques essais, j'en suis arrivé a faire le tracé mathématique d'un cercle par
cos et
sin. Restait à avoir les bons centres et rayons des 2 cercles: j'ai bien vu que le centre n'est pas placé pile sur un pixel entre les 4 pixels ! Sinon dommage pour moi mais je n'avais pas compris/comment utiliser correctement le
thêta... Après quelques essais, j'avais un rayon de
6.3 pixels pour le grand cercle,
4.5 pixels pour le petit, et un pas d'angle de
5°. Pourquoi
5°, car c'était la 1ère valeur qui m'a donné un cercle collant au bitmap, et qu'ensuite la valeur de
5 dans
C et la valeur de
A mise a
135 (°) pouvait me servir pour le zigzag ou pour d'autres angles
(2A=270=-90, 3A...).
Ensuite les rectangles : j'avais fait une première version avec les 2 pixels blancs : je me suis rendu vite compte que cela bouffait des octets ⇒ j'ai alors opté pour 3 rectangles pleins. Une petite optimisation ici a été de finir par le rectangle d'en haut et de finir sur le trait horizontal du haut du rectangle, et de finir dans la direction vers l'Est
(0°), afin de ne faire qu'un avancer de
22 pixels pour arriver sur le début du zigzag. J'avais réussi a faire une petite optimisation sur le zigzag, mais la participation totale n'étant pas meilleure, elle est passée à la trappe. Voir la
dernière participation.
Dans cette version je suis passé ensuite au nombre 2019, en essayant de limiter les nombres d'octets, en voyant que les
si finsi, voire les
si sinon finsi bouffait de la place ! J'ai essayé avec une boucle en tournant a droite pour la moitié haute du 2, puis autant de boucles que possible pour faire le reste du 2019 en tournant à gauche... sans oublier les saut entre chiffres que j'ai zappé exprès car moins rentables de les prendre en compte...
Pour le
logo en haut du cœur : j'ai essayé de regrouper les actions de même type
(éventuellement paramétré) : j'ai vu une symétrie d'axe verticale
( → variable D égale a ±1 agissant sur la position x), et une petite symétrie d'axe horizontal entre la pointe centrale haute et la pointe centrale basse du logo : variable
C agissant sur
y ! D'où le code.
Ben après pour le reste; l'épée et la tête : vu qu'il ne me restait plus beaucoup d'octets, j'ai tracé les plus grands traits, en essayant de lever le moins possible le crayon.
Après cela j'avais essayé de coder les mouvements, mais cela s'est révélé moins meilleur !
Voila, si vous avez des questions, demandez !

(message original)
3. Le
programme de
Krevo_ (
TI-Planet,
Planète Casio) à 2805 points nous emmène de nouveau sur le terrain du calcul. Une partie des constantes a clairement été générée, et on retrouve beaucoup de
Ent(X÷10) permettant de parcourir tous les chiffres d'un nombre. Alors, une idée ? Eh oui vous ne rêvez pas, ce programme a été compressé en encodant de façon compacte les pas ou les angles à suivre dans des grosses constantes pour éviter de répéter les instructions de déplacement élémentaires ! La logique de décodage occupe une majeure partie de cette soumission qui n'hésite pas à éluder les parenthèses fermantes non nécessaires dans les caculs pour réduire la quantité de code. Tout y est décrocher pour la 3ème place de l'épreuve !



Krevo_ a écrit :Alors pour les 2 cercles, j'ai fait :
4,5→A
Répéter 2
0→M
Stylo relevé
Répéter 32
Aller à x=6,5+Acos(M; y=-6,5+Asin(M
Stylo écrit
M+90÷8→M
⤴
6,4→A
⤴
C'est un peu pareil que
Grosged, j'ai un rayon de
4,5 pour le cercle intérieur, puis
6,4 pour le cercle extérieur. Ensuite j'ai
32 tours de la boucle interne car je fait progresser l'angle
M de
90°/8 (32x90°/8=4x90°=360°).
(La progression de l'angle et le rayon du cercle extérieur : tout ça c'est des réglages un peu empirique en vérifiant que ça dessinais bien les pixels voulus). Je dessine tout simplement un point aux coordonnées
(centre + rayon x cos angle ; centre + rayon x sin angle). Et effectivement, j'aurais gagné des octets en utilisant
θ.

Je passe sur la boucle qui dessine les
Z c'est trivial.
Pour les 3 rectangles, les chiffres et surtout Link et son épée, j'ai fait une sorte de moteur de dessin vectoriel
(qui existe donc 3 fois en tout, j'aurais sans doute pu coder les déplacement de stylo et optimisé mais bon c'était déjà consommateur de temps tout ça...). Il s'agit de consommer un à un les chiffres des variable
A et
M (je me limite à 15 chiffres suite à différents test pour voir ce qui marchais en nombre de chiffre significatif, c'est à dire sans perdre d'informations).
Stylo écrit
1343282468656→A
7833249394235→M
Répéter 3
Si E=8 Alors
2453212124178→A
1821311311322→M
Fin
Répéter 15
S'orienter à 45(A-FEnt(A÷Fdegrés
Avancer de(M-FEnt(M÷F))(1+,41(2-PGCD(2;A-FEnt(A÷Fpixels
Ent(A÷F→A
Ent(M÷F→M
⤴
7463468745678→A
2232433151413→M
1+E→E
⤴
(Attention ici E valait 6 car j'avais fini de dessiné les Z comme ça, ... donc E=8 est le test du 3è tour de boucle, car ici j'ai 3 fois 15 chiffres pour A et pour M).
Dans
A, j'ai mis successivement les angles, l'unité est le
multiple de 45°. Ainsi, avec
2453212124178→A, les orientations sont successivement de
90° (2x45°),
180° (4x45°),
225° (5 x 45°), ... Dans
M je mets le nombre de pixels. Donc
2232433151413→M signifie qu'il faudra avancer de
2,
2,
3, ... pixels. A chaque fois un couple orientation/avancement en pixels. Problème : quand l'orientation est en diagonale
(45°, 135°, 225 °, ...) il faut avancer non pas de n pixels mais de n√2 pixels, donc si le chiffre de l'orientation est impair, on est en diagonale et je multiplie le nombre de pixels d'avancement par
1+1x0.41, ce qui fait
1.41. Sinon, si c'est pair, je multiplie le nombre de pixels d'avancement par
1+0x0.41, ce qui fait tout simplement
1. La parité est testée à l'aide du
PGCD du nombre testé et de
2 (le PGCD est 2 pour les nombres pairs, 1 pour les nombres impairs).
(
message original 1,
message original 2)
2. L'
algorithme suivant nous vient de
Grosged et défraie le classement en annonçant 400 points de décalage avec son poursuivant. La logique est décuplée par la possibilité d'écrire des tests sans
«Si ... alors». On remarque en effet que
Ent(cos(X)) vaut essentiellement 1 si
X=0 et 0 sinon
(pourvu que X soit petit). Et donc
Ent(cos(X-Y)) permet de tester efficacement si deux coordonnées sont égales. Combinée avec un système de compression similaire à celui de
Krevo_ mais plus compact, cette technique permet de factoriser très aggressivement le code ! Ce programme mérite amplement sa 2ème place et ses 3217 points.



Grosged a écrit :Je vais vous détailler la meilleure de mes participations. Mais parlons d'abord de quelques astuces.
Afin d'éviter les tests du genre
Si...Alors...Fin qui prennent plusieurs lignes
(ou qu'on ne peut parfois pas utiliser car au sein de 3 boucles imbriquées), l'idéal aurait été de pouvoir insérer des tests directement dans les calculs, comme par exemple...
A+(B=7)→C. La fx-92+ Spéciale Collège ne le permettant pas, j'ai rusé en utilisant
Ent(cos(. En effet, grâce à
cos(0)=1 , la valeur entière de
cos(B-7) sera égale à
1 si
B=7, ou à
0 si
B≠7. L'exemple précédent devient donc...
A+Ent(cos(B-7→C (vous remarquerez , au passage, cette mini-optimisation qui consiste à ne pas refermer les parenthèses en fin de ligne  )
).
Autre astuce d'optimisation : parfois on a besoin de ne modifier que la variable
x ou
y. Alors, en fonction de l'orientation actuelle du stylo, un simple
Avancer de ... pixels suffit
(prends moins d'octets qu'un "Aller à x=... ; y=..."). Et quand on est vraiment obligé d'utiliser
Aller à x=... ; y=... , on peut mettre un
x=x ou
y=y pour la variable qui ne
bouge pas.

Intéressante aussi cette variable d'orientation
θ dont la valeur sera retranchée de
360 (autant de fois que nécessaire) dès qu'elle dépasse
359.
θ est donc une variable modulo
360. C'est bon à savoir car, bien utilisée, ça nous évitera de la (re)paramétrer.

A noter que cette variable n'est accessible qu'au moyen de la touche OPTN.
Parfois, on peut aussi optimiser au niveau des
Stylo écrit /
Stylo relevé : l'idéal étant, bien sûr, de tracer le plus possible sans
relever.

Au sujet des boucles,
Répéter jusqu'à... n'est pas toujours indispensable. Quand on sait déjà combien de fois la boucle doit
tourner, un simple
Répéter... suffit.

Au sujet des données, on n'a
-à ma connaissance- pas d'autre choix que de stocker ça dans des variables, par exemple en base 2...10 ou autres..., et d'y
réinjecter d'autres valeurs au fur-et-à-mesure, au coeur de la/des boucle(s)...

Voilà pour les quelques astuces, maintenant passons au programme.
(Merci @Lephe pour l'animation  )
).
Ca commence par la routine traçant les 3 espèces de rectangles :
Aller à x=4; y=17
44→D
54843253→A
Stylo écrit
Répéter 24
Tourner de ↺90 degrés
,1Ent(A→A
Avancer de 10(A-Ent(A pixels
A+50(2031Ent(cos(A))+313064Ent(cos(,1-A→A
⤴
Stylo relevé
Ne faites pas attention au
44→D, c'est pour plus tard.

Là, j'ai pensé ça comme un pointeur qui va, tout au long du tracé, tourner à chaque fois, à
90° dans le sens inverse des aiguilles d'une montre. Il me restait alors à définir le meilleur point de départ, insérer les longueurs respectives de tracé dans la variable
A (en base 10). Ainsi, ça démarre avec un tracé de longueur
3, puis
5...
2...
3... etc
(d'où 54843253→A). Parfois le stylo fait du
sur place pour, par exemple, faire un demi-tour
(donc tracé de longueur 0). Et comme on n'a pas assez de place pour inclure d'un coup toutes les longueurs dans
A...
A+50(2031Ent(cos(A))+313064Ent(cos(,1-A→A réinjecte des données au fur et à mesure...
(factorisation pour grapiller 1 ou 2 octets  )
).
Puis, l'affichage du bonhomme :
J'ai pensé ça en affichage successif de
bandes verticales de 16 pixels, chacune codée en base 2
(en binaire, quoi). Il y a, au total, 15 bandes réelles car certaines, vers la fin, sont vierges
(par souci d'optimisation, les 14 premières sont codées par groupes de 2, donc 7 valeurs de 32 bits).
Avancer de 30 pixels
655364x→A
Répéter 21
Répéter 16
,5Ent(A→A
Aller à x=x; y=52-2θ÷45-Arcsin(A-Ent(A
Stylo écrit
Avancer de 0 pixels
Stylo relevé
Tourner de ↺ 22,5 degrés
⤴
Avancer de 1 pixels
A+12Ent(cos(x-52))+3301008851Ent(cos(x-38))+4258383057Ent(cos(x-40→A
A+2453574741Ent(cos(x-42))+1081671044Ent(cos(x-D→A
A+797186680Ent(cos(x-34))+878062140Ent(cos(x-36→A
⤴
655364x→A pour la 1ère bande de 32 bits, laquelle est un multiple de 32
(et x est justement à 32), ainsi on gagne un octet.

Comme vous pouvez le constater, on réinjecte des données suivant la position actuelle du pointeur
(bref, en fonction de l'abscisse x). Les 2 pixels flottants font partie de la toute dernière bande verticale, celle-ci apparaît en abscisse
x=52 après quelques bandes
vierges. Codée en binaire, elle vaut
12... d'où
12Ent(cos(x-52)).

J'utilise la variable
θ comme valeur offset pour l'ordonnée
y et lorsqu'on n'a pas de pixel à tracer, l'affichage se fait hors-écran. Lorsque
,5Ent(A→A décode en base 2,
A-Ent(A nous donne la valeur
0,5 si pixel, sinon
0. On gère le hors-écran grâce au fait qu'
Arcsin(0)=0 et
Arcsin(0.5)=30...
Arcsin(A-Ent(A est préférable à
30(A-Ent(A.
 Ensuite , l'affichage des zig-zags :
Ensuite , l'affichage des zig-zags :
Aller à x=x; y=22
Répéter 8
Aller à x=16; y=y+A
A-1-Ent(10sin(A→A
Stylo écrit
Avancer de-Apixels
⤴
Là, j'ai focalisé sur les tracés horizontaux uniquement
(les diagonales s'affichent d'elles-même puisque le tracé reste en continu). Un petit
Ent(10sin... me permet, une fois arrivé à la longueur de
6, de ne pas la dépasser.

J'utilise une valeur négative rien que pour ultérieurement réutiliser cette variable
A=-6.
 Puis, l'affichage de l'épée :
Puis, l'affichage de l'épée :
Aller à x=D; y=8
Stylo écrit
Aller à x=45; y=5
Aller à x=42; y=7
Aller à x=41; y=2
Avancer de 5 pixels
Aller à x=x; y=4
Aller à x=45; y=1
Aller à x=x; y=A
Aller à x=D; y=-7
Aller à x=42; y=A
Aller à x=x; y=1
Stylo relevé
J'ai fini par m'apercevoir qu'un affichage en tracé
classique s'avérait plus économique qu'en mode sprite !
(Dans un premier temps, j'avais opté pour un affichage en mode "sprite", et de manière symétrique par souci d'économie de donnée)
Maintenant, c'est au tour des 2 cercles :
4,5→A
Répéter 2
Répéter 45
Tourner de ↺ 8 degrés
Aller à x=,5+Acos(θ; y=,5+Asin(θ
Stylo écrit
⤴
Stylo relevé
6,35→A
⤴
Ensuite, l'affichage de 2019 :
5642465600→A
Aller à x=x; y=2
Répéter 5
Aller à x=20π; y=y-1
Répéter 12
,5Ent(A→A
Si A=Ent(A Alors
Stylo écrit
Avancer de 0 pixels
Stylo relevé
Fin
Avancer de 4÷3 pixels
⤴
A+16779094Ent(cos(A→A
⤴
L'astuce principale réside dans l'économie de données : on fait comme si les 4 caractères composant
2019 faisaient chacuns 3x5 pixels
(on fait abstraction du pixel de séparation entre chaque, l'affichage s'occupera de les "détacher", d'où le pas de 4/3  )
). Encore pour réduire la taille des données, cette fois-ci , on code le tout en inversion video
(si pixel il y a , valeur 0).
Et pour terminer, l'affichage du vaisseau suivi de l'espèce de coeur :
81923201→A
Répéter 12
Aller à x=70; y=y
Répéter 9
,5Ent(A→A
Répéter2
Aller à x=140-x; y=D-Arctan(A-Ent(A
Stylo écrit
Avancer de 0 pixels
Stylo relevé
⤴
Avancer de 1 pixels
⤴
D-1→D
A+33686470Ent(cos(D-41))+2364428Ent(cos(D-38))+263685Ent(cos(D-35→A
⤴
Là, j'ai opté pour un affichage symétrique
(donc presque 2x moins de données  )
). Cette fois, j'utilise
Arctan au lieu d'
Arcsin, uniquement par rapport à la variable
D préalablement définie.
Voili-voilà ! J'espère avoir été assez clair dans mes explications, si vous souhaitez des détails sur telle ou telle partie, n'hésitez pas à poster

Et surtout... Longue vie à la fx-92+ Spéciale Collège !
(hmmmm je sais : c'est juste une question de pile, haha  )
).
(message original)
1. Et c'est
Pavel (
TI-Planet,
Planète Casio) qui domine ce classement du haut de ses 3270 points. Le
programme très court n'a plus grand-chose d'humain et l'animation montre une méthode de tracé très orthodoxe. Après avoir tracé rapidement les cercles et les rectangles, il attaque le sprite de Link et les décorations colonne par colonne, pixel par pixel, s'arrêtant même sur l'herbe
(aussi tirée de la première génération de Pokémon) sur son passage. La méthode de chargement des données donne le vertige. J'ai cru un moment à une transformée de Fourier mais ne serait-ce pas un bitmap très bien écrit ? La méthode maître cette épreuve ne révèle pas facilement ses secrets. Une conclusion glorieuse !



Pavel a écrit :Mon idée initiale était que la méthode la plus simple serait de convertir l'image en colonnes de pixels, d'utiliser des bits pour représenter les pixels et de les dessiner pixel par pixel. Reste à trouver comment coder le plus efficacement les bits.
Étant donné que la hauteur de l'image est de 30 pixels, que 2^30 contient 10 chiffres décimaux et que la fx-92+ Spéciale Collège fonctionne avec des valeurs entières avec 10 chiffres décimaux, les colonnes de pixels peuvent être encodées sous forme de valeurs entières. Afin de convertir les colonnes de pixels en valeurs entières, j'ai écrit un petit script Python:
from scipy import misc
image = misc.imread('LWTC5q8.png')
d = 9
for y in range(85):
counter = 0
value = 0
for x in range(30):
if image[x+1,y+5,0] == 0:
counter += 1
value += 2**x
if counter > 1:
length = len(str(abs(value)))+ len(str(abs(y - d)))
if y - d == 0: length -= 2
print('%2d %2d %9d %2d' % (counter, length, value, y - d))
Ce script imprime le nombre de pixels par colonne, la valeur entière, le nombre de chiffres décimaux dans la valeur entière et la position de la colonne de pixels. La valeur
d=9 du déplacement horizontal de l'image est choisie pour minimiser la somme des longueurs de toutes les valeurs entières. Avec ce script, j'ai obtenu 52 valeurs entières correspondant à des colonnes de plus de 1 pixel.
Le code pour dessiner les colonnes de pixels est assez simple:
S'orienter à -90 degrés
Répéter 85
f(x) → B
Aller à x=x+1; y=9
Répéter 30
Si 1=PGCD(Ent(B÷2^(9-y)); 2) Alors
Stylo écrit
Avancer de 0 pixels
Stylo relevé
Fin
Avancer de 1 pixels
⤴
⤴
Reste à trouver comment programmer
f(x)→B, où
f(x) est une fonction qui renvoie une valeur entière correspondant à la colonne de pixels avec la coordonnée
x. En C ou en Python, cette fonction peut être programmée comme
123*(x==1)+456*(x==2)+789*(x==3)+.... La seule façon de programmer quelque chose de similaire sur la fx-92+ Spéciale Collège que j'ai pu trouver est la suivante :
123*Ent(Cos(x-1)) + 456*Ent(Cos(x-2)) + 789*Ent(Cos(x-3))+.... En utilisant cette approche, j'ai réussi à obtenir 3025 points avec
ce code.
Malheureusement, même si cette approche est facile à implementer, elle n'est pas la plus efficace. J'ai compris ça quand
grosged a soumis une solution avec un score plus élevé et j'ai commencé à chercher des méthodes plus optimales pour dessiner certaines parties de l'image. Voyant que je vais devoir tester beaucoup de codes différents et qu'il faudra beaucoup de temps pour les saisir manuellement, j'ai écrit un script Python pour programmer automatiquement l'émulateur fx-92+ Spéciale Collège :
https://gitea.planet-casio.com/Pavel/fx92-programmer . En utilisant ce script, j'ai rapidement testé différentes approches pour dessiner les zig-zags, les cercles et les rectangles. Ensuite, j'ai combiné les meilleures parties de tous les codes que j'ai réussi à produire et j'ai obtenu
une solution correspondant à 3270 points.
Après la publication des solutions de ce défi, j'ai analysé le code écrit par grosged et j'ai été impressionné par sa solution très efficace pour dessiner les rectangles. J'ai immédiatement voulu vérifier quel score pouvait être obtenu en combinant une approche similaire pour dessiner les rectangles avec d'autres parties de mon code et j'ai réussi à obtenir 3309 points avec
ce code.
Conclusion et choix des lots
Encore plus que l'année dernière, ces participations révèlent l'ingéniosité avec laquelle vous avez approché le sujet. Les techniques utilisées dépassent de loin nos attente. Bravo !

Comme prévu par le réglement du concours, les 12 participants ayant obtenu les meilleurs scores vous pouvoir choisir les lots de leur choix par ordre de score. Le premier à se lancer est donc
Pavel. Vous pouvez suivre le choix en parallèle sur ce fil et sur TI-Planet. Lorsque votre tour vient, postez sur l'un des forums pour annoncer votre choix.
 À bientôt sur Planète Casio !
À bientôt sur Planète Casio !  Article connexe sur TI-Planet : Résultat concours de rentrée 2019 - défi de tracé
Article connexe sur TI-Planet : Résultat concours de rentrée 2019 - défi de tracé


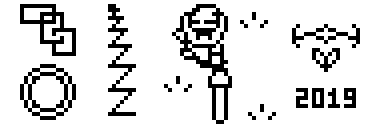









 ) je n'ai fait que quelques tests que j'aurais essayé d'optimiser. Une de mes participations où l'on peut voir un peu de ce code est : ici. Le principe retenu est que chaque pixel dessiné vaut 1 et chaque pixel non dessiné vaut 0. Mon idée était d'encoder l'image colonne par colonne en transformant le binaire obtenu en décimal et de le stocker dans une variable. Ensuite avec une boucle pour chaque colonne je décodais la variable en binaire point par point et j'affichai le pixel si la valeur était 1 sinon ne je l'affichais pas. Le code parlera mieux que mes explications.
) je n'ai fait que quelques tests que j'aurais essayé d'optimiser. Une de mes participations où l'on peut voir un peu de ce code est : ici. Le principe retenu est que chaque pixel dessiné vaut 1 et chaque pixel non dessiné vaut 0. Mon idée était d'encoder l'image colonne par colonne en transformant le binaire obtenu en décimal et de le stocker dans une variable. Ensuite avec une boucle pour chaque colonne je décodais la variable en binaire point par point et j'affichai le pixel si la valeur était 1 sinon ne je l'affichais pas. Le code parlera mieux que mes explications.











 ), j'ai utilisé la symétrie centrale de la zone centrale mais en traçant la figure ligne par ligne (comme des lignes horitontales de pointillés) puis j'ai tracé les deux parenthèses et enfin les deux traits obliques manquants.
), j'ai utilisé la symétrie centrale de la zone centrale mais en traçant la figure ligne par ligne (comme des lignes horitontales de pointillés) puis j'ai tracé les deux parenthèses et enfin les deux traits obliques manquants.














 ). La variable B vaut 0 lors du premier tour de boucle, puis 1 au second. Celle-ci permet de bien placer ma symétrie : en effet, l'axe de symétrie du visage se situe ENTRE 2 pixels. Si je n'utilisais pas B, la symétrie se tracerait 1 pixel plus loin, autour d'un axe de symétrie qui se situerai alors SUR une verticale de pixels. B me permet ainsi de déplacer de 1 pixel toute ma symétrie. Enfin, C est simplement une valeur qui revient souvent (2A+B) et cela me permet de gagner des octets en initialisant une fois C et la réutiliser au lieu de taper à chaque fois 2A+B. Pour finir, j'ai pivoté au tout début de mon programme de 270 degrés (c'est à dire en vertical vers le bas) pour économiser des Aller à et les remplacer simplement par des Avancer de lorsque j'avais besoin d'aller vers le bas.
). La variable B vaut 0 lors du premier tour de boucle, puis 1 au second. Celle-ci permet de bien placer ma symétrie : en effet, l'axe de symétrie du visage se situe ENTRE 2 pixels. Si je n'utilisais pas B, la symétrie se tracerait 1 pixel plus loin, autour d'un axe de symétrie qui se situerai alors SUR une verticale de pixels. B me permet ainsi de déplacer de 1 pixel toute ma symétrie. Enfin, C est simplement une valeur qui revient souvent (2A+B) et cela me permet de gagner des octets en initialisant une fois C et la réutiliser au lieu de taper à chaque fois 2A+B. Pour finir, j'ai pivoté au tout début de mon programme de 270 degrés (c'est à dire en vertical vers le bas) pour économiser des Aller à et les remplacer simplement par des Avancer de lorsque j'avais besoin d'aller vers le bas. )
)





 ) à dessiner correctement le bitmap.
) à dessiner correctement le bitmap.
 Du coup une fois passé sur émulateur, je ne suis plus revenu sur le python/ordi !
Du coup une fois passé sur émulateur, je ne suis plus revenu sur le python/ordi !







 ).
).
 A noter que cette variable n'est accessible qu'au moyen de la touche OPTN.
A noter que cette variable n'est accessible qu'au moyen de la touche OPTN.


 ).
). Là, j'ai pensé ça comme un pointeur qui va, tout au long du tracé, tourner à chaque fois, à 90° dans le sens inverse des aiguilles d'une montre. Il me restait alors à définir le meilleur point de départ, insérer les longueurs respectives de tracé dans la variable A (en base 10). Ainsi, ça démarre avec un tracé de longueur 3, puis 5... 2... 3... etc (d'où 54843253→A). Parfois le stylo fait du sur place pour, par exemple, faire un demi-tour (donc tracé de longueur 0). Et comme on n'a pas assez de place pour inclure d'un coup toutes les longueurs dans A... A+50(2031Ent(cos(A))+313064Ent(cos(,1-A→A réinjecte des données au fur et à mesure... (factorisation pour grapiller 1 ou 2 octets
Là, j'ai pensé ça comme un pointeur qui va, tout au long du tracé, tourner à chaque fois, à 90° dans le sens inverse des aiguilles d'une montre. Il me restait alors à définir le meilleur point de départ, insérer les longueurs respectives de tracé dans la variable A (en base 10). Ainsi, ça démarre avec un tracé de longueur 3, puis 5... 2... 3... etc (d'où 54843253→A). Parfois le stylo fait du sur place pour, par exemple, faire un demi-tour (donc tracé de longueur 0). Et comme on n'a pas assez de place pour inclure d'un coup toutes les longueurs dans A... A+50(2031Ent(cos(A))+313064Ent(cos(,1-A→A réinjecte des données au fur et à mesure... (factorisation pour grapiller 1 ou 2 octets  ).
).
 J'utilise la variable θ comme valeur offset pour l'ordonnée y et lorsqu'on n'a pas de pixel à tracer, l'affichage se fait hors-écran. Lorsque ,5Ent(A→A décode en base 2, A-Ent(A nous donne la valeur 0,5 si pixel, sinon 0. On gère le hors-écran grâce au fait qu'Arcsin(0)=0 et Arcsin(0.5)=30... Arcsin(A-Ent(A est préférable à 30(A-Ent(A.
J'utilise la variable θ comme valeur offset pour l'ordonnée y et lorsqu'on n'a pas de pixel à tracer, l'affichage se fait hors-écran. Lorsque ,5Ent(A→A décode en base 2, A-Ent(A nous donne la valeur 0,5 si pixel, sinon 0. On gère le hors-écran grâce au fait qu'Arcsin(0)=0 et Arcsin(0.5)=30... Arcsin(A-Ent(A est préférable à 30(A-Ent(A. 
 J'utilise une valeur négative rien que pour ultérieurement réutiliser cette variable A=-6.
J'utilise une valeur négative rien que pour ultérieurement réutiliser cette variable A=-6. 
 ). Encore pour réduire la taille des données, cette fois-ci , on code le tout en inversion video (si pixel il y a , valeur 0).
). Encore pour réduire la taille des données, cette fois-ci , on code le tout en inversion video (si pixel il y a , valeur 0). ). Cette fois, j'utilise Arctan au lieu d'Arcsin, uniquement par rapport à la variable D préalablement définie.
). Cette fois, j'utilise Arctan au lieu d'Arcsin, uniquement par rapport à la variable D préalablement définie. Et surtout... Longue vie à la fx-92+ Spéciale Collège ! (hmmmm je sais : c'est juste une question de pile, haha
Et surtout... Longue vie à la fx-92+ Spéciale Collège ! (hmmmm je sais : c'est juste une question de pile, haha  ).
).





Citer : Posté le 09/11/2019 11:25 | #
Merci, félicitations à tous !
Donc oui, @Pavel, qu'est-ce que tu nous prends ?
Citer : Posté le 09/11/2019 11:39 | #
Bien joué à tous !
Pavel mais quelle prestation dans ces concours ! Franchement bravo
(Et de toute façon, vous pouvez pas dire le contraire)
MultipliCasio
RDM Calculs
Back Mirror
A Switch To The Top C
Citer : Posté le 09/11/2019 12:43 | #
Déjà, bravo énorme travail de rédaction pour cette annonce des résultats !!
Citer : Posté le 09/11/2019 12:54 | #
Pavel a choisi le lot avec la nouvelle TI-Nspire CX II-T CAS : https://tiplanet.org/forum/viewtopic.php?f=49&t=23114&p=247720#p247718
C'est au tour de @grosged maintenant.
Citer : Posté le 09/11/2019 13:12 | #
Déjà, bravo énorme travail de rédaction pour cette annonce des résultats !!
Merci ! J'ai rédigé les petits commentaires et Critor a écrit le reste et tout mis en page. Ça permet de répartir sensiblement bien le travail
J'ai également ajouté une description de la solution de LePetitMage qui l'a partagée sur TiP !
Citer : Posté le 09/11/2019 14:13 | #
Félicitation à tous et à toutes !
Citer : Posté le 09/11/2019 19:29 | #
J'ai ajouté une description de la solution de Afyu qu'il a envoyé par mail.
Citer : Posté le 09/11/2019 20:27 | #
grosged a choisi le lot avec la nouvelle TI-Nspire CX II-T : https://tiplanet.org/forum/viewtopic.php?f=49&t=23114&p=247757#p247753
C'est à toi @Krevo_. Que veux-tu parmi ce qui nous reste ?
https://tiplanet.org/forum/viewtopic.php?f=49&t=23114&p=247757#p247757
Citer : Posté le 09/11/2019 20:47 | #
C'est à toi @Krevo_. Que veux-tu parmi ce qui nous reste ?
Pour le choix du lot, je choisis ... de ne rien prendre (et je demande que mon choix soit respecté sans poser de questions et sans essayer de m'influencer pour prendre quand même quelquechose)
J'estime avoir été déjà bien servi dans les 12 derniers mois :
- en décembre 2018, j'ai gagné une Casio graph 90+E au concours de l'avent de Planète Casio.
- en juillet 2019, j'ai gagné une Casio graph 35+E II sur Facebook avec LeProfDuWeb.
Je suis donc correctement doté en calculatrices par rapport à mes besoins et ne suis pas interessé par les différents goodies. Je souhaite que les lots du concours profitent aux autres participants.
Ce fût un vrai plaisir pour moi de participer à ce défi de tracé.
Citer : Posté le 09/11/2019 20:55 | #
C'est tout à ton honneur, nous ne pouvons que nous incliner.
Il restera donc un lot pour le 13ème, il faudra qu'il te remercie.
Citer : Posté le 09/11/2019 20:58 | #
Si preuve il fallait que le concours est aussi une bonne dose de fun... et bien en voilà.
Je suis vraiment content que le problème t'ait intéressé même sans la perspective des lots. Je pense que tu ne sera pas déçu par le puzzle de cette année
Citer : Posté le 09/11/2019 21:57 | #
C'est à toi @Krevo_. Que veux-tu parmi ce qui nous reste ?
Pour le choix du lot, je choisis ... de ne rien prendre (et je demande que mon choix soit respecté sans poser de questions et sans essayer de m'influencer pour prendre quand même quelquechose)
J'estime avoir été déjà bien servi dans les 12 derniers mois :
- en décembre 2018, j'ai gagné une Casio graph 90+E au concours de l'avent de Planète Casio.
- en juillet 2019, j'ai gagné une Casio graph 35+E II sur Facebook avec LeProfDuWeb.
Je suis donc correctement doté en calculatrices par rapport à mes besoins et ne suis pas interessé par les différents goodies. Je souhaite que les lots du concours profitent aux autres participants.
Ce fût un vrai plaisir pour moi de participer à ce défi de tracé.
Bravo
Passé ici il y a peu. ಥ‿ಥ
Jouez à Mario sans arrêt sur votre Casio !
City Heroes
Piano Casio
Micro GIMP
Citer : Posté le 10/11/2019 15:12 | #
Astrostellar nous a envoyé une description de sa solution, que j'ai ajoutée à l'article !
Ajouté le 10/11/2019 à 15:16 :
... et de même pour Encephalogramme au passage. Merci pour toutes les infos ! o/
Ajouté le 10/11/2019 à 17:42 :
Ajouté deux petites notes de Clément et Éléonore sur leurs participations.
Ajouté le 10/11/2019 à 22:49 :
Ajouté les explications d'Edgar 13. On frôle les 0.1 Mo de texte quand même